\( \newcommand{\bm}[1]{\boldsymbol{#1}} \)

Chapter 9 Spatial Survival Models

There are several excellent resources to assist with learning survival analysis. For population-based cancer data, Dickman, Lambert, and Hakulinen (2018) is a recommended resource which was extensively used in preparing this chapter.

9.1 Survival Analysis

Survival is one of the most important measures of cancer patient care. When used in conjunction with other measures, it can give insight into diagnosis and treatment.

Survival analysis is synonymous with time-to-event analysis. In the cancer patient context, possible events of interest could be:

  • Death
  • Relapse
  • Hospital discharge

Death is the most common event of interest. There are three requirements that must be satisfied:

  • Agreed scale for the measurement of time
  • Unambiguous origin of time (e.g. cancer diagnosis)
  • Precise occurrence of the event of interest (e.g. death)

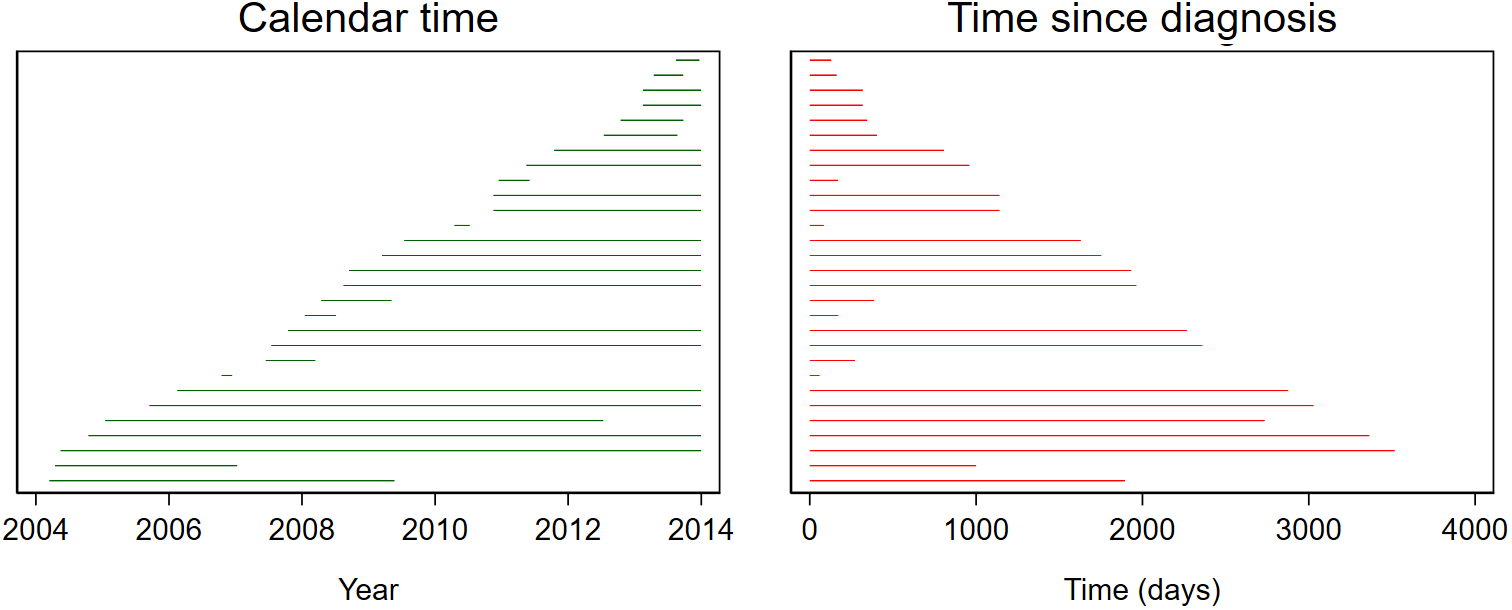
To compute the time-to-event, the time between the origin (date of diagnosis) and the event (date of death) is measured. However, not all patients will have experienced the event of interest by the end of the study period. Records for patients who have been diagnosed but have not experienced the event by the end of the study period are censored. This censoring is a key feature of survival data, and it requires specialised models. Calendar time itself is of little interest in survival analyses – it is the duration between diagnosis and the event or censoring that is key. The following image illustrates how calendar time is converted to time since diagnosis such that the origin always starts at 0. Each horizontal line represents an individual. The line begins when the individual was diagnosed and ends when the individual experienced an event or was censored.

Survival can be expressed as either the survival proportion (the proportion who do not experience the event) or the event rate. The survival function \(S(t)\) represents the probability of surviving longer than time \(t\).

The event (hazard) rate is proportional to the rate at which the survival function decreases: \[ h(t) = -\frac{d}{dt}\text{ln}S(t) \\ S(t) = \exp \left\{ -\int_0^t h(u) du \right\} = \exp\left(-H(t)\right) \] where \(h(t)\) is the instantaneous hazard and \(H(t)\) is the cumulative (or integrated) hazard.

Two additional ways to characterise a survival probability distribution include:

  • The probability density function: \(f(t) = h(t)S(t)\) This is the probability of the event per time unit.

  • The cumulative density function: \(F(t) = 1- \exp(-H(t))\) This is the cumulative probability of the event occurring, and represents the area under the \(f(t)\) curve between 0 and \(t\).

Once you have one measure, you can obtain any of them.

9.2 Measuring Survival

For nonparametric estimation of survival:

  1. Split follow-up into small intervals of time, e.g. 1 year, 1 month or each time an event occurs
  2. Estimate conditional probabilities of surviving an interval. (This is called ‘conditional’ because the person has to have survived up to that interval) \[p_i = 1-\frac{d_i}{n_i}\]
  3. \(S(t)\) is the product of the conditional probabilities up to time \(t\). \[S(t_k) = \prod_{i=1}^k p_i\]

For step 1, if there are both events (deaths) and censoring within a small time interval, then there are two approaches available:

  • Kaplan-Meier: assume the event comes before the censoring, i.e. everyone is at risk when the events occur. (Time interval ends when event occurs).
  • Actuarial/life table: assume half the censored individuals are at-risk when the events occur.

9.2.1 The Actuarial Method

  1. Split the data into a series of time intervals and estimate the conditional probability in each time interval.
    If no censoring: \(p=(n-d)/n\)
    If censoring: \(p=(n'-d)/n'\) where \(n'=n-0.5w\)
    (this assumes censoring occurs uniformly throughout the interval).
  2. Multiply the conditional survival proportions together.

where \(n\) is the number alive at the start of the interval, \(d\) is the number of deaths during the interval, \(n'\) is the effective number of patients at risk during the interval, and \(w\) is the number censored during the interval.

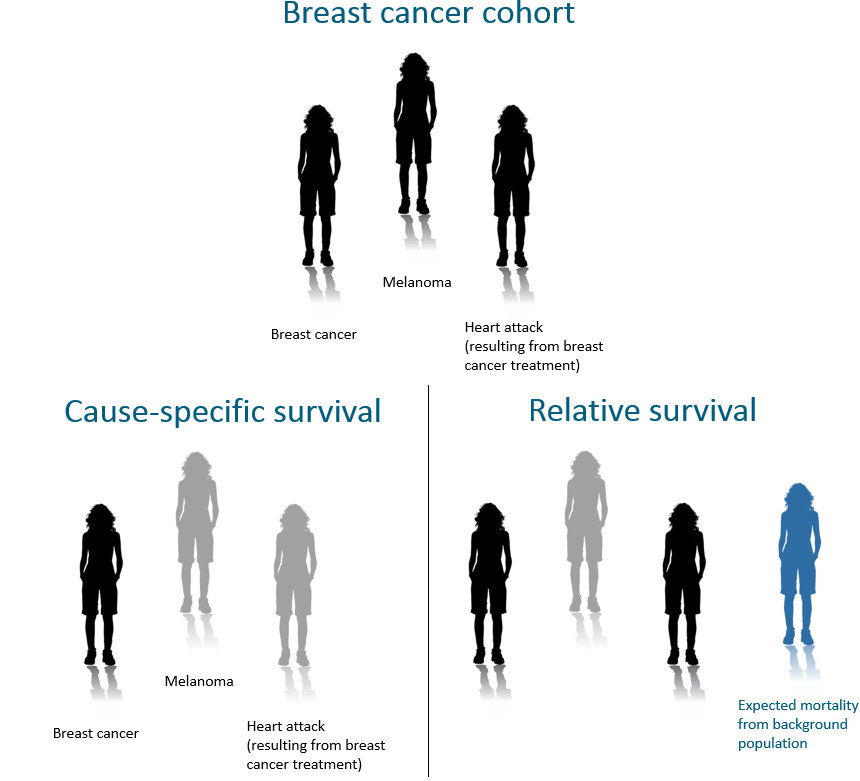
9.2.2 All-cause Survival vs Net Survival

When all deaths are counted as an event, this is called all-cause survival. The problems with all-cause survival are :

  • Improvements over time may mean less deaths to cancer, or it may mean less deaths to other causes.
  • Bias differs by age - older ages have very high non-cancer mortality.

But there are alternative ways to measure survival, which differ in the definition of events and censoring:

  • All-cause survival: any death is an event
  • Net survival (hypothetical world where no one can die from anything other than cancer)
    • Cause-specific: any cancer-specific death according to the death certificate is an event. Individuals whose deaths were not related to the specific type of cancer are considered censored at the date of death.
    • Relative: any death is an event. Individuals who are still alive are censored. The calculated expected population mortality is then subtracted from all deaths. Although this is supposed to only reflect deaths in a cancer-free population, because rates of cancer tend to be low, most analyses use mortality rates from the entire population.

The following figure illustrates these survival methods. Here, one death is expected based on population mortality rates (shown in blue), so this is subtracted to give two deaths attributed to breast cancer (shown in black). This differs from cause-specific survival where only one death was attributed to breast cancer. Although both cause-specific and relative survival are aiming to capture the same measure (net survival), sometimes cause-specific can under-estimate deaths due to cancer. If the implied assumptions (see Section 9.4) are met, then both relative survival and cause-specific survival measures should be quite similar.

9.3 Describing the Results

Suppose you obtain a 5-year net survival estimate of 70% for bowel cancer in New Zealand. The way this is reported depends on how it was calculated. For instance:

  • Cause-specific: New Zealanders have a 70% probability of surviving bowel cancer for at least 5 years.
  • Relative: New Zealanders diagnosed with bowel cancer are 70% as likely to survive for at least 5 years compared to the general population (of same age, sex, time period etc).
    Cause-specific or relative: 70% of New Zealanders diagnosed with bowel cancer are alive after 5 years in the hypothetical situation where bowel cancer is the only possible cause of death.

However, when net survival estimates are reported in the media, reports and even many research publications, the ‘hypothetical scenario’ caveat is typically discarded from the description, using phrases such as ‘x% of cancer patients survived for five years’. Alternatively, many just state that ‘5-year relative survival was x%’ without further elaboration, leaving the reader to interpret the reported estimate (Baade et al. 2016).

9.4 Assumptions

Note the following implied assumptions:

  • Cause-specific: accurate classification of cause of death
  • Relative: appropriate estimation of expected survival (accurate population and population-mortality data)

Both require assuming independence, i.e. no factors influence both cancer and non-cancer mortality other than factors controlled for.

The independence assumption may be violated by:

  • smoking (although this has little impact on lung cancer estimation due to short survival times (Hinchliffe et al. 2012))
  • older ages

There is no way to test for the independence assumption. Controlling for these factors therefore becomes more important

Why is independence needed for mortality? If there are factors that influence both cancer mortality and non-cancer mortality that have not been controlled for in the analysis then cause-specific survival does not have a probability interpretation.

There are a range of approaches to calculating both cause-specific and relative survival:

The 3 most commonly used methods are: Ederer I and II, and Hakulinen. These differ in how they define expected survival. Expected survival can be thought of as being calculated for a cohort of patients from the general population matched by age, sex, and time period. The methods differ regarding how long each individual is considered to be ‘at risk’ for the purpose of estimating expected survival.

  • Ederer I: the matched individuals are considered to be at risk indefinitely (even beyond the closing date of the study). The time at which a cancer patient dies or is censored has no effect on the expected survival.
  • Ederer II: the matched individuals are considered to be at risk until the corresponding cancer patient dies or is censored.
  • Hakulinen: if the survival time of a cancer patient is censored then so is the survival time of the matched individual. However, if a cancer patient dies the matched individual is assumed to be ‘at risk’ until the closing date of the study.

For most software, the default setting is to use Ederer II. Although Pohar Perme has strong advocates for its use and is theoretically unbiased, it can be more erratic in its estimates over long follow-up times and it has increased variation (the variance-bias trade-off). For short-term survival analysis, we are likely to obtain similar results regardless of method chosen.

9.5 Data Required and Software

There are many survival packages in R. Survival uses specific notation (developed by Terry Therneau), and most packages use this: Surv(time = ovarian$futime, event = ovarian$fustat)

The following data are required depending on the chosen measure of survival (note that area of residence is only needed when doing small-area analyses):

  • Cause-specific survival:
    • Disease incidence data, preferably at the individual-level - patient’s age, sex, date diagnosed, area of residence, as well as if they died, and if so, death date and the cause of death (cancer of interest or other).
  • Relative survival:
    • Disease incidence data, preferably at the individual-level - patient’s age, sex, date diagnosed, area of residence, as well as if they died, and if so, death date.
    • Total mortality data - number of deaths in each age group, sex, time and area.
    • Population data by age group, sex, time and area.

In either case, for a small-area analysis, we also need a file specifying the boundaries of our areas, to create an adjacency matrix file.

9.6 Modelling Relative Survival

Dickman et al. (2004), Hakulinen (1982), and others have promoted the relative survival model in the framework of GLMs.

\[ d_i \sim \text{Poisson}(\mu_i) \\ \log(\mu_i - d_i^*) = \log(y_i) + \bm{x}^{\text{T}}\bm{\beta} \]

where \(\mu_i - d_i^*\) represents excess deaths, \(y_i\) is the person-time at risk, and \(\bm{x}\) is a vector of covariates.

In this model the number of deaths in each age group, follow-up year and area are assumed to follow a Poisson distribution. Since \(d^*\) is the expected number of deaths due to other causes, so \(\mu - d^*\) represents the excess mortality due to the cancer.

The excess mortality is determined by the \(y_i\) person-time at risk in the \(i^{\text{th}}\) observation, and \(\beta\) the coefficient of the predictor variable vector \(x\) (you may like to include broad age groups, or cancer stage, or other important prognostic factors).

Most analyses of cancer registry data will use relative survival, and this model can work well if you are wanting to look at cancer across a large area, such as all of New Zealand.

As can be seen, modelling of relative survival is really modelling the excess hazard. Given you can calculate relative survival estimates without modelling, the aim of modelling is to enable additional adjustment for and quantify the influence of factors of interest. One main advantage for our purposes is to be able to compare results against additional Bayesian models, and ensure the estimates for beta remain consistent.

To calculate the input model data in R:

  1. Population mortality data
    • Read in the number of deaths and number of population by age, year, sex (area, etc).
      • If numbers are large, you may want to use single year ages.
      • If numbers are small, you may want to group years, ages etc and assign the same rate to everything in that group.
    • Calculate age-specific rates.
    • Use lifetable to calculate probability of surviving.
    • Save as population mortality datasets.
  2. Calculate \(d\), \(d^*\) and \(y\).
    • Read in the cancer data.
    • Check the data.
    • Create a subset of cancer data to be included in the analyses. Common exclusions in Australia are:
      • Diagnosed by death certificate (DCO cases) or autopsy (Some cancer registries exclude those with basis of diagnosis unknown, but AIHW does not).
      • Unknown age at diagnosis.
      • Zero survival time (death date = diagnosis date).
      • Apparent age at censoring date \(\geq\) 116.
    • Perform the calculation. There are many options within R, and the choice depends on your data characteristics and analysis aims. For instance, if you have individual-level data, one simple way is to define a Lexis object (from package Epi) and use survtab (from the popEpi package). For pre-aggregated data, you can instead use the survtab_ag function. Other options include the relsurv package, or if you want to have a smooth baseline, use the rstpm2 package. If you only have duration between diagnosis and death in months, then use the period function from the periodR package (available from: http://www.krebsregister.saarland.de/improve/periodR_en.html).

A Lexis object is a data frame with additional attributes that allows the multiple time dimensions of follow-up (such as age, calendar time, or time since an event) to be managed. Lexis objects are named after the German demographer Wilhelm Lexis (1837-1914), who is credited with the invention of the “Lexis diagram” for representing population dynamics simultaneously by several timescales.

Survival is one of the most important measures of cancer patient care. Everyone wants to know about it: clinicians, patients, researchers, politicians, etc. But each of these groups have different needs.

Both cause-specific and relative survival is useful for comparing populations independent of background mortality. These measures are important for researchers, government and policy makers. However, hypothetical world scenarios are often not of great interest to cancer patients or clinicians.

Check out Interpret Cancer Survival: https://interpret.le.ac.uk/ for ideas on alternative ways to show survival.

9.7 (Fully) Bayesian Relative Survival Modelling

Only a few published papers have examined spatial Bayesian relative survival models, and these include:

  • Fairley et al. (2008) combined the GLM as recommended by Paul Dickman with the BYM model.
  • Hennerfeind, Held, and Sauleau (2008) used splines..
  • Cramb, Mengersen, and Baade (2011b) and also Cramb et al. (2012) were based on Fairley’s model.
  • Saez et al. (2012) was also the same as Fairley.
  • Cramb et al. (2016) altered Fairley’s model to incorporate restricted cubic splines so that the baseline was smooth.

The survival model implemented for the ACA was the Bayesian spatial relative survival model based on that by Fairley et al. (2008), but with a Leroux CAR prior on the SRE, \(S_i\):

\[ d_{itk} \sim \text{Poisson}(\mu_{itk}) \\ \log(\mu_{itk} - d_{itk}^*) = \log(y_{itk}) + \alpha_t + x_{ik}\beta_k + S_i \]

where \(i = 1, 2, \ldots, 2148\) SA2s, \(t = 1, 2, \ldots, 5\) follow-up years, and \(k = 1,2,3\) broad age groups.

9.8 Example OpenBUGS Code

9.8.1 Queensland Cancer Atlas

This is the BUGS 4 code used in the Queensland Cancer Atlas (https://cancerqld.org.au/research/queensland-cancer-statistics/queensland-cancer-atlas/), and was based on Fairley et al. (2008).

model{
# Likelihood
    for (i in 1:N.d) { 
         d[i]  ~ dpois(mu[i]) 
        mu[i] <- d.star[i] + d.excess[i]
        log(d.excess[i]) <-  log(y[i])+alpha[RiskYear[i]] + beta[1]*agegp2[i] + 
            beta[2]*agegp3[i] + v[Area[i]] + u[Area[i]]
    }
    
    # CAR prior distribution for spatial random effects: 
    u[1:N] ~ car.normal(adj[], weights[], num[], tau.u)     
    for (k in 1:sumNumNeigh) {weights[k] <- 1 }
        
    # Normal prior distribution for the uncorrelated heterogeneity:
    for (j in 1:N) {
        v[j] ~ dnorm(0, tau.v)
        smoothed[j] <- v[j]+u[j]
        EHR[j] <- exp(smoothed[j])  # Excess hazard ratio
    }
                   
    # Other priors           
    tau.v ~ dgamma(0.1, 0.01)   sigma.v2 <- 1/tau.v
    tau.u ~ dgamma(0.1, 0.01)   sigma.u2con <- 1/tau.u
    sigma.u2marginal <- sd(u[])*sd(u[])
    fracspatial <- sigma.u2marginal/(sigma.u2marginal + sigma.v2)
        
    for (t in 1:T) {alpha[t] ~ dnorm (0, 0.001)}
    for (k in 1:N.beta) {beta[k] ~ dnorm(0, 0.001)}
}

By defining \(\mu\), the linear predictor can be called excessd, rather than \(\mu - d^*\).

The prior distributions are then listed, along with the calculation of the excess hazard ratio (EHR), which was the exponential of the sum of the structured and unstructured random effect components, \(u_i\) and \(v_i\) respectively, and this was what we mapped.

Both \(\alpha\) and \(\beta\) were given priors with vague normal distributions (mean of zero and variance of 1 million). Vague priors were also given to both gamma distributions with shape parameter 0.1 and scale parameter of 100, which equates to a mean of 10 and variance of 1000.

9.8.2 Australian Cancer Atlas

For the Australian Cancer Atlas, we used the same basic model 5, but instead of using BYM, we used a Leroux spatial prior. Unlike the ICAR prior, WinBUGS/OpenBUGS does not include a built-in Leroux prior so it needed to be manually coded. The full model specification in the BUGS language is given below:

model{ 
    for(i in 1:N.d){
        d[i] ~ dpois(mu[i])
        mu[i] <- d.star[i] + d.excess[i]
        log(d.excess[i]) <- log(y[i]) + alpha[RiskYear[i]] + beta[1] * agegp2[i] + 
            beta[2] * agegp3[i] + beta[3] * agegp4[i] + s[Area[i]]
    }
    
    # Leroux prior for spatial effects
    for(j in 1:N){
        s[j] ~ dnorm(mean.s[j], prec.s[j])
        A[j] <- (rho * num[j] + 1 - rho)
        prec.s[j] <- A[j] / sigma.s2
        mean.s[j] <- rho * sum(W.s[cum[j] + 1:cum[j+1]]) / A[j]
    }
    for (h in 1:sumnum) {
        W.s[h] <- s[adj[h]]
    }
    
    # Other priors
    sigma.s2 ~ dnorm(0, 0.2)T(0,)
    rho ~ dunif(0, 1)
    
    for(t in 1:T){               # flat prior on intercept
        alpha[t] ~ dnorm(0, 0.01) 
    }
    
    for(k in 1:3){
        beta[k] ~ dnorm(0, 0.01)
    }
}

# In the example code below, this model is saved as "Leroux.txt"

Note that our hyperpriors were more tightly constrained than for the Queensland Cancer Atlas, and this is consistent with advice on hyperpriors at: https://github.com/stan-dev/stan/wiki/Prior-Choice-Recommendations.

The key R code in forming these data inputs are:

# Fixed values
bugs.dat <- list(
    N = 2148,            # Number of areas (SA2s)
    T = 5,               # Number of risk years
    N.d = N.d,           # Number of data rows
    d = d,               # Number of deaths
    d.star = d.star,     # Expected number of deaths due to causes other than cancer of interest
    y = y,               # Person-time at risk offset
    RiskYear = RiskYear,
    Area = Area,
    adj = adj.data$adj,
    num = adj.data$num,
    cum = c(cumsum(adj.data$num) - adj.data$num, sum(adj.data$num)),
    sumnum = sum(adj.data$num),
    agegp2 = x1,
    agegp3 = x2,
    agegp4 = x3
)

# Initial values
inits <- function(){list(
    alpha = rep(-3, 5),
    u = rep(0, N),
    sigma.u2 = 0.2,
    rho = 0.5,
    beta = rep(0, 3)
)}

# Fit the model using WinBUGS/OpenBUGS
bugs(
    data = bugs.dat,
    inits = inits,
    parameters.to.save = c("alpha", "u", "sigma.u2", "beta", "rho"),
    model.file = "Leroux.txt",
    n.chains = 1,
    n.iter = 150000,
    n.burnin = 50000,
    n.thin = 10,
)

where adj.data was obtained from the shapefile in the same way as shown in Sections 7.3 and 8.3.

9.9 Worked Examples

9.9.1 Actuarial Method

In this example, we import some fictitious data which contains values of \(n\), \(d\), \(w\) at 10 intervals (refer to Section 9.2).

Exercises:

  1. Compute the values of \(n'\), \(p\) and \(S(t)\) (as additional columns).
  2. Calculate 1, 5, and 10-year survival using the actuarial method.
# Import data
data <- read.csv("Downloaded Data/9.9.1 Actuarial Method.csv")
head(data)
##   Interval  n d w
## 1    [0-1) 35 7 1
## 2    [1-2) 27 1 3
## 3    [2-3) 23 5 4
## 4    [3-4) 14 2 1
## 5    [4-5) 11 0 1
## 6    [5-6) 10 0 0
# Exercise 1
data$n.dash <- with(data, n - 0.5 * w)
data$p <- with(data, (n.dash - d)/n.dash)
data$S <- with(data, cumprod(p))
data
##    Interval  n d w n.dash         p         S
## 1     [0-1) 35 7 1   34.5 0.7971014 0.7971014
## 2     [1-2) 27 1 3   25.5 0.9607843 0.7658426
## 3     [2-3) 23 5 4   21.0 0.7619048 0.5834991
## 4     [3-4) 14 2 1   13.5 0.8518519 0.4970548
## 5     [4-5) 11 0 1   10.5 1.0000000 0.4970548
## 6     [5-6) 10 0 0   10.0 1.0000000 0.4970548
## 7     [6-7) 10 0 3    8.5 1.0000000 0.4970548
## 8     [7-8)  7 0 1    6.5 1.0000000 0.4970548
## 9     [8-9)  6 1 4    4.0 0.7500000 0.3727911
## 10   [9-10)  1 0 1    0.5 1.0000000 0.3727911
# Exercise 2
data$S[1]           # 1-year survival
## [1] 0.7971014
data$S[5]           # 5-year survival
## [1] 0.4970548
data$S[10]          # 10-year survival
## [1] 0.3727911

9.9.2 Kaplan-Meier Method

This example has been adapted from several sources, including (most prominently) https://rpubs.com/alecri/258589. (This link covers additional material to that presented here).

In this example, we use the orca data set, which contains data on 338 patients diagnosed with an oral squamous cell carcinoma (OSCC), collected between January 1, 1985 and December 31, 2005 from the two northernmost provinces of Finland.

Follow-up of patients was started on the date of cancer diagnosis and ended on the date of death, migration, or the closing date of the follow-up, December 31, 2008. Cause of death was classified into the 2 categories:

  1. deaths from OSCC; and
  2. deaths from other causes.

First, let’s examine the data.

# Import data
orca <- read.table("http://www.stats4life.se/data/oralca.txt")
head(orca)
##   id    sex      age stage  time          event
## 1  1   Male 65.42274  unkn 5.081          Alive
## 2  2 Female 83.08783   III 0.419 Oral ca. death
## 3  3   Male 52.59008    II 7.915    Other death
## 4  4   Male 77.08630     I 2.480    Other death
## 5  5   Male 80.33622    IV 2.500 Oral ca. death
## 6  6 Female 82.58132    IV 0.167    Other death
# Tabulate values of event
table(orca$event, exclude = NULL)   # Include records w/ missing values
## 
##          Alive Oral ca. death    Other death 
##            109            122            107
# Interactive plot to examine survival time and end
orca <- mutate(orca, text = paste(
        "Subject ID = ", id, "<br>", 
        "Time = ", time, "<br>", 
        "Event = ", event, "<br>", 
        "Age = ", round(age, 2), "<br>", 
        "Stage = ", stage
    ))

ggplotly(
    ggplot(orca, aes(x = id, y = time, text = text)) +
        geom_linerange(aes(ymin = 0, ymax = time)) +
        geom_point(aes(shape = event, color = event), stroke = 0.3, cex = 2) +
        scale_shape_manual(values = c(1, 3, 4)) +
        labs(y = "Time (years)", x = "Subject ID") + 
        coord_flip() + 
        theme_classic(),
    tooltip = "text"
)

Exercises:

  1. Calculate 1, 5, and 10-year survival using the Kaplan-Meier method.
  2. Repeat exercise 1 using the actuarial method.

To estimate the survival function using the Kaplan-Meier method, we need the follow-up time since diagnosis until death (or censoring), and the patients’ status (dead or alive). The Kaplan-Meier estimate can be computed using the Surv and survfit functions from the survival package. Surv creates a survival object (essentially a reformatted two-column data.frame containing the time and status variables); survfit then estimates the survival function.

# Exercise 1
# Indicator variable for whether status is censored
orca <- mutate(orca, censored = event == "Alive")
table(orca$censored, exclude = NULL)
## 
## FALSE  TRUE 
##   229   109
# Create survival object
status <- !orca$censored    # TRUE = dead, FALSE = alive
S <- Surv(orca$time, status)

# Etimate the survival function using the Kaplan-Meier method
fit_KM <- survfit(S ~ 1, data = orca)
print(fit_KM, print.rmean = TRUE)
## Call: survfit(formula = S ~ 1, data = orca)
## 
##        n events rmean* se(rmean) median 0.95LCL 0.95UCL
## [1,] 338    229   8.06     0.465   5.42    4.33    6.92
##     * restricted mean with upper limit =  23.3
# 1, 5, and 10-year survival
summary(fit_KM, times = c(1, 5, 10))    # "survival" column
## Call: survfit(formula = S ~ 1, data = orca)
## 
##  time n.risk n.event survival std.err lower 95% CI upper 95% CI
##     1    274      64    0.811  0.0213        0.770        0.854
##     5    145      95    0.515  0.0279        0.463        0.573
##    10     68      39    0.349  0.0292        0.297        0.412

We can also create a plot of the estimated survival function using ggsurvplot() from the survminer package.

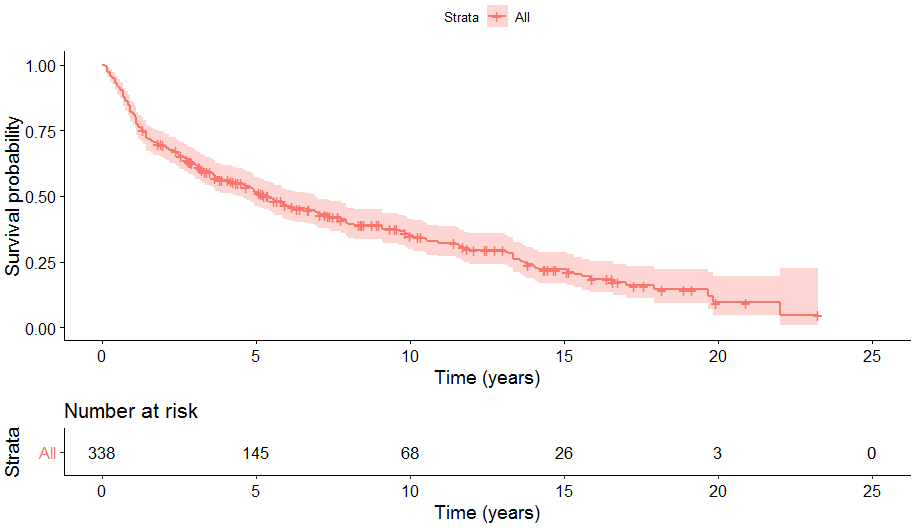
# Visualise survival function
ggsurvplot(fit_KM, risk.table = TRUE, xlab = "Time (years)", censor = TRUE, data = orca)

(There appears to be a bug in ggsurvplot when used in Rmarkdown which causes a run-time error. So a static image of the output has been included here.)

For exercise 2, we first need to create aggregated data, i.e. divide the follow-up in groups and calculate in each strata the number of people at risk, events, and censored. Then the survival function using the actuarial method is estimated using the lifetab function from the KMsurv package.

# Exercise 2
# Create life table
cuts <- 0:23
lifetab_dat <- mutate(orca, time_cat = cut(time, cuts)) %>%
    group_by(., time_cat) %>%
    summarise(., nlost = sum(censored == TRUE), nevent = sum(censored == FALSE))

# Actuarial estimation using lifetab function
actuarial <- with(lifetab_dat, lifetab(
    tis = cuts, 
    ninit = nrow(orca), 
    nlost = nlost, 
    nevent = nevent)
)
actuarial <- round(actuarial, 4)

# 1, 5, and 10-year survival
actuarial[c(1, 5, 10) +1,]         # "surv" column
##       nsubs nlost nrisk nevent   surv    pdf hazard se.surv se.pdf se.hazard
## 1-2     274     4   272     41 0.8107 0.1222 0.1630  0.0213 0.0179    0.0254
## 5-6     145    14   138     13 0.5146 0.0485 0.0989  0.0279 0.0131    0.0274
## 10-11    68     4    66      5 0.3505 0.0266 0.0787  0.0291 0.0116    0.0352
# Note that the actuarial function reports the survival estimates at the start of the interval shown, i.e. the X-year survival corresponds to the interval [X-1, X]. So to get the X-year survival, we need to add 1.

# Compare this with the KM estimates above.

We can compare the estimated survival functions using ggplot (and optionally ggplotly)

# Coerce KM fit output into data.frame
dat_KM <- summary(fit_KM) %>%
    with(., data.frame(time, n.risk, n.event, n.censor, surv, std.err, lower, upper))

# Visualise survival functions
ggplotly(
    ggplot() +
        geom_step(data = dat_KM, aes(x = time, y = surv, colour = "K-M")) +
        geom_step(data = actuarial, aes(x = cuts[-length(cuts)], y = surv,
            colour = "LT")) +
        labs(x = "Time (years)", y = "Survival", colour = "Estimator") +
        theme_classic()
)

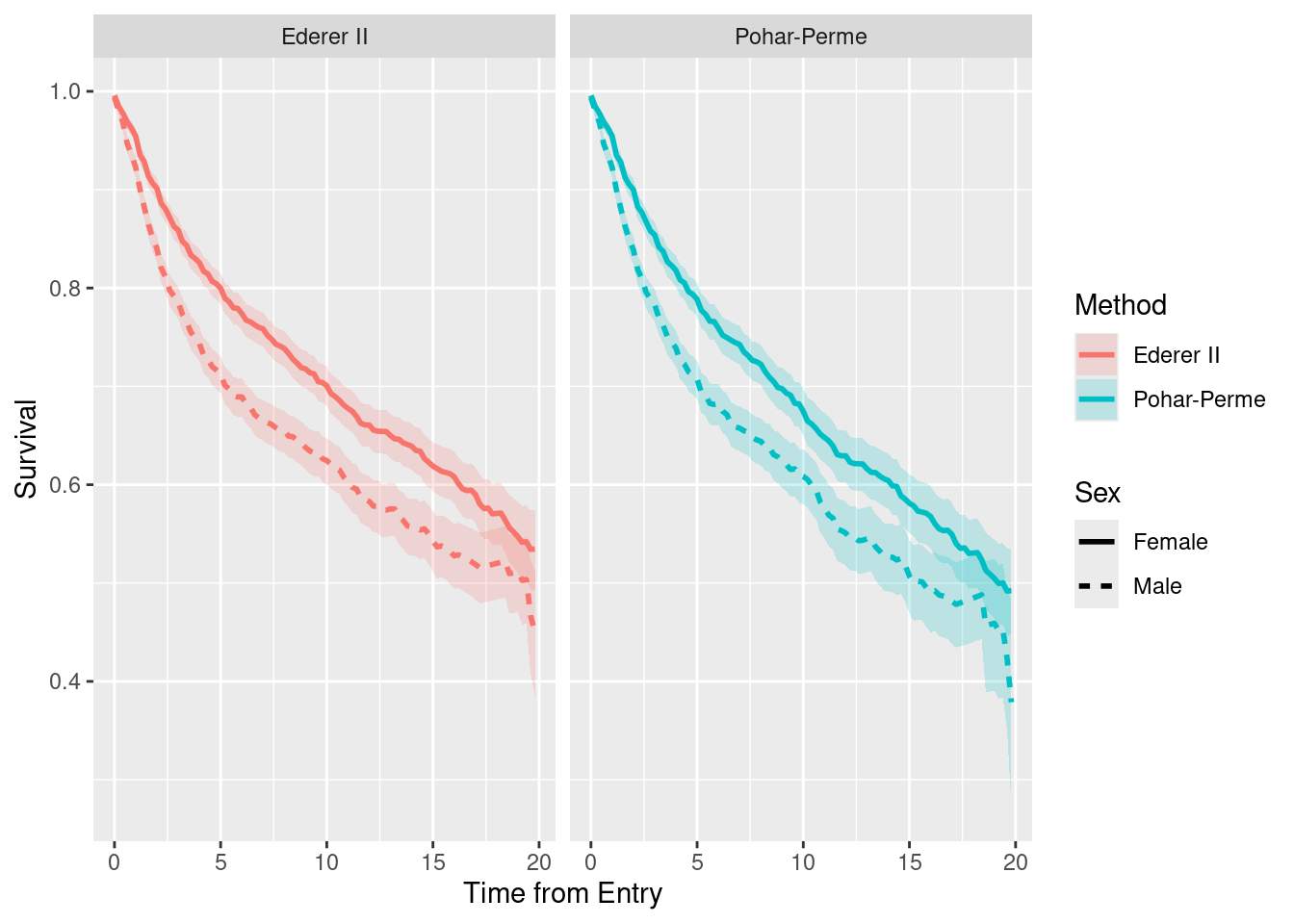
9.9.3 Ederer II and Pohar-Perme Methods

This worked example is adapted from https://cran.r-project.org/web/packages/popEpi/vignettes/survtab_examples.html.

# Import population mortality data
data(popmort, package = "popEpi")   # Population mortality rates in Finland, 1951-2013
names(popmort)[3] <- "age"
head(popmort)
##      sex  year   age         haz
##    <int> <int> <int>       <num>
## 1:     0  1951     0 0.036363176
## 2:     0  1951     1 0.003616547
## 3:     0  1951     2 0.002172384
## 4:     0  1951     3 0.001581249
## 5:     0  1951     4 0.001180690
## 6:     0  1951     5 0.001070595
# Import cancer data
data(sire, package = "popEpi")      # A simulated cohort of Finnish female rectal cancer patients
head(sire)
##      sex    bi_date    dg_date    ex_date status   dg_age
##    <int>     <IDat>     <IDat>     <IDat>  <int>    <num>
## 1:     1 1952-05-27 1994-02-03 2012-12-31      0 41.68877
## 2:     1 1959-04-04 1996-09-20 2012-12-31      0 37.46378
## 3:     1 1958-06-15 1994-05-30 2012-12-31      0 35.95616
## 4:     1 1957-05-10 1997-09-04 2012-12-31      0 40.32055
## 5:     1 1957-01-20 1996-09-24 2012-12-31      0 39.67745
## 6:     1 1962-05-25 1997-05-17 2012-12-31      0 34.97808
# Pretend some are male
set.seed(1)
sire$sex <- rbinom(nrow(sire), 1, 0.5)

# Create Lexis object
x <- Lexis(
    entry = list(FUT = 0, age = dg_age, year = get.yrs(dg_date)), 
    exit = list(year = get.yrs(ex_date)), 
    data = sire[sire$dg_date < sire$ex_date, ],
    exit.status = factor(status, levels = 0:2, labels = c("alive", "canD", "othD")),
    merge = TRUE
)
## NOTE: entry.status has been set to "alive" for all.
# View Lexis object
head(x)
##  lex.id FUT   age    year lex.dur lex.Cst lex.Xst sex    bi_date    dg_date    ex_date status dg_age
##       1   0 41.69 1994.09   18.91   alive   alive   0 1952-05-27 1994-02-03 2012-12-31      0 41.689
##       2   0 37.46 1996.72   16.28   alive   alive   0 1959-04-04 1996-09-20 2012-12-31      0 37.464
##       3   0 35.96 1994.41   18.59   alive   alive   1 1958-06-15 1994-05-30 2012-12-31      0 35.956
##       4   0 40.32 1997.67   15.33   alive   alive   1 1957-05-10 1997-09-04 2012-12-31      0 40.321
##       5   0 39.68 1996.73   16.27   alive   alive   0 1957-01-20 1996-09-24 2012-12-31      0 39.677
##       6   0 34.98 1997.37   15.63   alive   alive   1 1962-05-25 1997-05-17 2012-12-31      0 34.978

In the Lexis object, separate variables for current and exit state allows representation of multistate data.

It is straightforward to estimate various survival time functions with survtab once a Lexis object has been defined. The code below demonstrates two different ways to compute the observed survival time function for 5 years follow-up (FUT = follow-up time).

# Observed survival - explicit method.
st.obs <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex, 
    data = x, 
    surv.type = "surv.obs", 
    breaks = list(FUT = seq(0, 5, 1/12)),
    pophaz = popmort
)

# Observed survival - easy method (assumes lex.Xst in x is the status variable)
st.obs <- survtab(
    FUT ~ sex, 
    data = x, 
    surv.type = "surv.obs",
    breaks = list(FUT = seq(0, 5, 1/12)), 
    pophaz = popmort
)

To use the period method instead, use “year” in the breaks, with the years indicating the at-risk period, e.g. If the at-risk period was 2000-2005, then use breaks = list(FUT = seq(0, 5, 1/12), year = c(2000, 2005)).

Note that this interval is interpreted as 1 Jan 2000 to 31 Dec 2004. This is because years are considered to be fractional, i.e. c(2000, 2005) is translated in R as c(2000.0001, 2004.9999). So if you want an at-risk period instead spanning 1 Jan 2000 to 31 Dec 2005, you need to specify the years as c(2000, 2006).

The observed survival time function gives us the key input data for our models, namely:

  • Observed number of deaths, \(d\) = st.obs$d
  • Expected number of deaths due to other causes, \(d^*\) = st.obs$d.exp
  • Person-year at risk offset, \(y\) = st.obs$pyrs

survtab can also be used to compute relative survival functions. The following code estimates the survival function using the Ederer II and Pohar-Perme methods.

# Relative survival - Ederer II method
st.e2 <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex, 
    data = x, 
    surv.type = "surv.rel", 
    relsurv.method = "e2",
    breaks = list(FUT = seq(0, 5, 1/12)),
    pophaz = popmort
)

# Relative survival - Pohar-Perme method
st.pp <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex, 
    data = x, 
    surv.type = "surv.rel", 
    relsurv.method = "pp",
    breaks = list(FUT = seq(0, 5, 1/12)),
    pophaz = popmort
)

# Compare relative survival methods
dat <- data.frame(
    s = c(st.obs$surv.obs,     st.e2$r.e2,    st.pp$r.pp),
    lo = c(st.obs$surv.obs.lo, st.e2$r.e2.lo, st.pp$r.pp.lo),
    hi = c(st.obs$surv.obs.hi, st.e2$r.e2.hi, st.pp$r.pp.hi),
    time = st.obs$Tstart,
    sex = st.obs$sex,
    Method = rep(1:3, each = nrow(st.obs))
)
dat$sex <- factor(dat$sex, labels = c("Male", "Female"))
dat$Method <- factor(dat$Method, labels = c("Observed", "Ederer II", "Pohar-Perme"))

ggplot(dat, aes(x = time, y = s, colour = Method, fill = Method, group = sex)) +
    geom_line(aes(linetype = factor(sex)), size = 1) +
    geom_ribbon(aes(ymin = lo, ymax = hi), alpha = 0.5, colour = NA) +
    facet_grid( ~ Method) +
    labs(x = "Time from Entry", y = "Survival") +
    scale_linetype("Sex")

Exercises:

  1. Compute the relative survival function using the Ederer II and Pohar-Perme methods for the “colon” data set.
  2. Repeat exercise 1 using the “melanoma” data set.

The variables in the “popmort”, “colon”, and “melanoma” data sets are described in Appendix B.1.

# Exercise 1
# Import population mortality data
popmort <- readRDS("Downloaded Data/9.9.3 popmort.rds")
head(popmort)
##    sex year age    prob         haz
## 1 Male 1951   0 0.96429 0.036363177
## 2 Male 1951   1 0.99639 0.003616547
## 3 Male 1951   2 0.99783 0.002172384
## 4 Male 1951   3 0.99842 0.001581249
## 5 Male 1951   4 0.99882 0.001180690
## 6 Male 1951   5 0.99893 0.001070595
# Import cancer data
colon <- readRDS("Downloaded Data/9.9.3 colon.rds")
head(colon)
##      sex AGE     stage mmdx yydx surv_mm surv_yy       status                subsite        year8594
## 1 Female  77   Distant    3 1977    16.5     1.5 Dead: cancer             Transverse Diagnosed 75-84
## 2 Female  78 Localised    7 1978    82.5     6.5  Dead: other   Coecum and ascending Diagnosed 75-84
## 3   Male  78   Distant   10 1978     1.5     0.5 Dead: cancer Descending and sigmoid Diagnosed 75-84
## 4   Male  76   Distant   10 1976     1.5     0.5 Dead: cancer Descending and sigmoid Diagnosed 75-84
## 5   Male  80 Localised   12 1980     8.5     0.5 Dead: cancer Descending and sigmoid Diagnosed 75-84
## 6 Female  75 Localised   11 1975    23.5     1.5 Dead: cancer   Coecum and ascending Diagnosed 75-84
##   agegrp         dx       exit id
## 1    75+ 1977-03-04 1978-07-20  1
## 2    75+ 1978-07-26 1985-06-11  2
## 3    75+ 1978-10-10 1978-11-25  3
## 4    75+ 1976-10-28 1976-12-13  4
## 5    75+ 1980-12-20 1981-09-05  5
## 6    75+ 1975-11-16 1977-11-01  6
# Remove unecessary columns, otherwise survtab won't work
popmort$prob <- NULL

# Create Lexis object
x <- Lexis(
    entry = list(FUT = 0, age = AGE, year = get.yrs(dx)), 
    exit = list(year = get.yrs(exit)), 
    data = colon[colon$dx < colon$exit, ],
    exit.status = status,
    merge = TRUE
)
## NOTE: entry.status has been set to "Alive" for all.
# Relative survival - Ederer II method
st.e2 <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex, 
    data = x, 
    surv.type = "surv.rel", 
    relsurv.method = "e2",
    breaks = list(FUT = seq(0, 20, 0.2)),
    pophaz = popmort
)

# Relative survival - Pohar-Perme method
st.pp <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex, 
    data = x, 
    surv.type = "surv.rel", 
    relsurv.method = "pp",
    breaks = list(FUT = seq(0, 20, 0.2)),
    pophaz = popmort
)

# Compare relative survival methods
dat <- data.frame(
    s = c(st.e2$r.e2,     st.pp$r.pp),
    lo = c(st.e2$r.e2.lo, st.pp$r.pp.lo),
    hi = c(st.e2$r.e2.hi, st.pp$r.pp.hi),
    time = st.e2$Tstart,
    sex = st.e2$sex,
    Method = rep(1:2, each = nrow(st.e2))
)
dat$Method <- factor(dat$Method, labels = c("Ederer II", "Pohar-Perme"))

ggplot(dat, aes(x = time, y = s, colour = Method, fill = Method, group = sex)) +
    geom_line(aes(linetype = factor(sex)), size = 1) +
    geom_ribbon(aes(ymin = lo, ymax = hi), alpha = 0.2, colour = NA) +
    facet_grid( ~ Method) +
    labs(x = "Time from Entry", y = "Survival") +
    scale_linetype("Sex")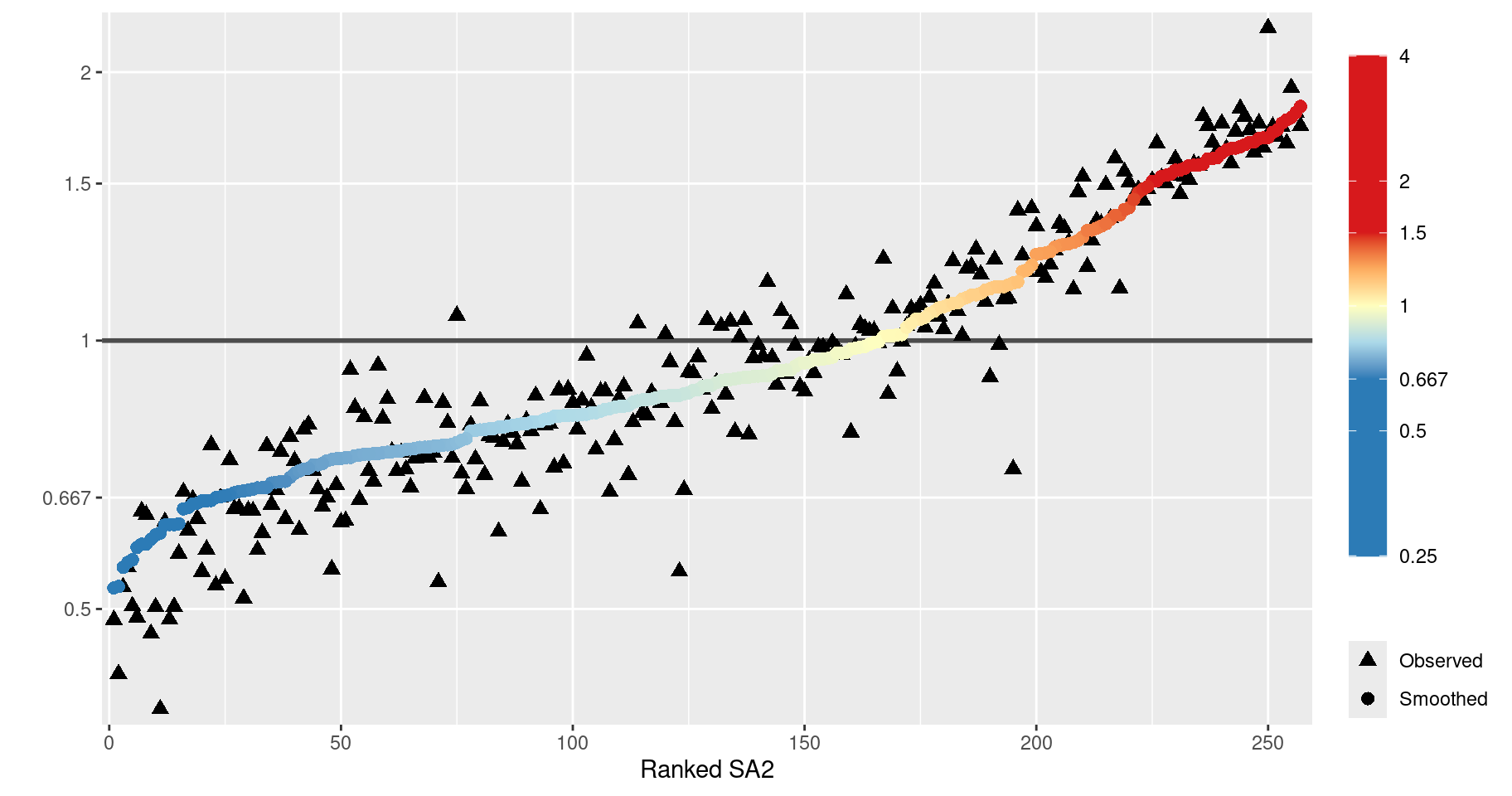

# Exercise 2
# Import cancer data (use the same popmort data)
mel <- readRDS("Downloaded Data/9.9.3 melanoma.rds")
head(mel)
##      sex age     stage mmdx yydx surv_mm surv_yy       status          subsite        year8594
## 1 Female  81 Localised    2 1981    26.5     2.5  Dead: other    Head and Neck Diagnosed 75-84
## 2 Female  75 Localised    9 1975    55.5     4.5  Dead: other    Head and Neck Diagnosed 75-84
## 3 Female  78 Localised    2 1978   177.5    14.5  Dead: other            Limbs Diagnosed 75-84
## 4 Female  75   Unknown    8 1975    29.5     2.5 Dead: cancer Multiple and NOS Diagnosed 75-84
## 5 Female  81   Unknown    7 1981    57.5     4.5  Dead: other    Head and Neck Diagnosed 75-84
## 6 Female  75 Localised    9 1975    19.5     1.5 Dead: cancer            Trunk Diagnosed 75-84
##           dx       exit agegrp id
## 1 1981-02-02 1983-04-20    75+  1
## 2 1975-09-21 1980-05-07    75+  2
## 3 1978-02-21 1992-12-07    75+  3
## 4 1975-08-25 1978-02-08    75+  4
## 5 1981-07-09 1986-04-25    75+  5
## 6 1975-09-03 1977-04-19    75+  6
# Create Lexis object
x <- Lexis(
    entry = list(FUT = 0, age, year = get.yrs(dx)),
    exit = list(year = get.yrs(exit)),
    data = mel[mel$dx < mel$exit, ],
    exit.status = status,
    merge = TRUE
)
## NOTE: entry.status has been set to "Alive" for all.
# Relative survival - Ederer II method
st.e2 <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex,
    data = x,
    surv.type = "surv.rel",
    relsurv.method = "e2",
    breaks = list(FUT = seq(0, 20, 0.2)),
    pophaz = popmort
)

# Relative survival - Pohar-Perme method
st.pp <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex,
    data = x,
    surv.type = "surv.rel",
    relsurv.method = "pp",
    breaks = list(FUT = seq(0, 20, 0.2)),
    pophaz = popmort
)

# Compare relative survival methods
dat <- data.frame(
    s = c(st.e2$r.e2,     st.pp$r.pp),
    lo = c(st.e2$r.e2.lo, st.pp$r.pp.lo),
    hi = c(st.e2$r.e2.hi, st.pp$r.pp.hi),
    time = st.e2$Tstart,
    sex = st.e2$sex,
    Method = rep(1:2, each = nrow(st.e2))
)
dat$Method <- factor(dat$Method, labels = c("Ederer II", "Pohar-Perme"))

ggplot(dat, aes(x = time, y = s, colour = Method, fill = Method, group = sex)) +
    geom_line(aes(linetype = factor(sex)), size = 1) +
    geom_ribbon(aes(ymin = lo, ymax = hi), alpha = 0.2, colour = NA) +
    facet_grid( ~ Method) +
    labs(x = "Time from Entry", y = "Survival") +
    scale_linetype("Sex")

9.9.4 An in-depth Relative Survival Example, Start to Finish

Exercises:

  1. Import population mortality data set “9.9.4 popmort.rds” and prepare it for further use.
  2. Import the cancer data set “9.9.4 cancer.rds” and make the following modifications:
    • Exclude records where death date < diagnosis date.
    • Exclude records that are death certificate only (DCO) cases and where age is missing or > 116 (these ages are unlikely to be correct). (Refer to the data dictionary in Appendix B.2.)
  3. Create the Lexis object for the cancer data set.
  4. Compute the sex-specific relative survival function for 5 years follow-up using Ederer II for the ‘at-risk’ period 1 Jan 2000 to 31 Dec 2007.
  5. Visualise the relative survival function.
  6. Fit a relative survival GLM model to this data (this will require a non-standard link function (Holleczek and Brenner 2013), \(\log(\mu - d^*)\)):
    1. by sex.
    2. by sex and broad agegroups (bagegroup).
  7. Compare the modelled relative survival estimates in Exercise 6a against the unmodelled results in Exercise 4. (Hint: extract the linear predictor from the GLM, remove the offset, and compute the sex- and interval-specific relative survival rates. The relative survival function is then the cumulative product of these rates.)

The variables in the “popmort”, and “cancer” data sets are described in Appendix B.2.

# Exercise 1
# Import population mortality data
popmort <- readRDS("Downloaded Data/9.9.4 popmort.rds")
head(popmort)
##   year    sex agegroup grid count pop
## 1 1997 Female        1    1     1  26
## 2 1997 Female        2    1     1  36
## 3 1997 Female        3    1     1  27
## 4 1997 Female        4    1     1  13
## 5 1997 Female        5    1     0  28
## 6 1997 Female        6    1     0  32
# Aggregate over all areas
popmort <- summaryBy(count + pop ~ year + sex + agegroup, FUN = sum, data = popmort)

# Add hazard rate
popmort$haz <- popmort$count.sum/popmort$pop.sum

# Expand to single year age groups (lifetable only tested on single-year ages)
popmort <- expandRows(popmort, count = 5, count.is.col = FALSE)
row.names(popmort) <- NULL
popmort$dummyvar <- 1:5
popmort$age <- (popmort$agegroup * 5) - popmort$dummyvar

# Order by year, then sex, then age
popmort <- popmort[order(popmort$year, popmort$sex, popmort$age),]

# Remove unecessary columns, otherwise survtab won't work
popmort <- popmort[, c(1, 2, 6, 8)]
head(popmort)
##    year    sex         haz age
## 5  1997 Female 0.002811351   0
## 4  1997 Female 0.002811351   1
## 3  1997 Female 0.002811351   2
## 2  1997 Female 0.002811351   3
## 1  1997 Female 0.002811351   4
## 10 1997 Female 0.002087075   5
# Exercise 2
# Import cancer data
cancer1 <- readRDS("Downloaded Data/9.9.4 cancer.rds")
head(cancer1)
##      id    sex year site10group death age bagegroup grid   fu_date      exit     dxdate    dthdate
## 1 12715   Male 1999           1     1  81         3   39 08oct2005 08oct2005 2005-11-17 2005-10-08
## 2 10693   Male 2000           1     1  88         3  352 04jan2001 04jan2001 2001-01-06 2001-01-04
## 3  5040   Male 2002           1     1  17         1  172 04may2002 04may2002 2002-05-26 2002-05-04
## 4  4064   Male 2002           1     0  43         1  449 31dec2007 31dec2007 2002-09-15       <NA>
## 5 10486 Female 2007           1     0  57         2  232 31dec2007 31dec2007 2007-02-15       <NA>
## 6  8459   Male 2002           1     1  71         3  287 17feb2003 17feb2003 2002-06-15 2003-02-17
##        exit_ surv basis
## 1 2005-10-08  -40     8
## 2 2001-01-04   -2     6
## 3 2002-05-04  -22     8
## 4 2007-12-31 1933     8
## 5 2007-12-31  319     8
## 6 2003-02-17  247     8
# Exclude records where death date < diagnosis date.
cancer1 <- subset(cancer1, subset = dthdate > dxdate | dxdate < exit_)

# Exclude DCO cases and where age > 116
cancer1 <- subset(cancer1, subset = basis < 10 & age <= 116)
# Exercise 3
# Rename variables in cancer1 so they differ from those in Lexis object
names(cancer1)[c(3, 6)] <- toupper(names(cancer1)[c(3, 6)])

# Create Lexis object
x <- Lexis(
    entry = list(FUT = 0, age = AGE, year = get.yrs(dxdate)),
    exit = list(year = get.yrs(exit_)),
    data = cancer1,
    exit.status = death,
    merge = TRUE
)
## NOTE: entry.status has been set to 0 for all.
# Remove duplicate variables
x[,which(names(x) %in% c("YEAR", "AGE"))] <- NULL
# Exercise 4
# Relative survival - Ederer II, 'at-risk' period of 2000-2007
st.e2 <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex,
    data = x,
    surv.type = "surv.rel",
    relsurv.method = "e2",
    breaks = list(FUT = seq(0, 5, 1/12), year = c(2000, 2008)),
    pophaz = popmort
)
# Exercise 5
# Visualise relative survival function
ggplot(st.e2, aes(x = Tstart, y = r.e2, colour = factor(sex), fill = factor(sex), 
        group = sex)) +
    geom_line(aes(linetype = factor(sex)), size = 1) +
    geom_ribbon(aes(ymin = r.e2.lo, ymax = r.e2.hi), alpha = 0.2, colour = NA) +
    labs(x = "Time from Entry", y = "Survival") +
    scale_linetype("Sex") +
    scale_fill_discrete("Sex") +
    scale_colour_discrete("Sex")

Recall the key input data for the model is given in the st.e2 object:

  • Observed number of deaths, \(d\) = st.e2$d
  • Expected number of deaths due to other causes, \(d^*\) = st.e2$d.exp
  • Person-year at risk offset, \(y\) = st.e2$pyrs
# Exercise 6
# Define non-standard link function
modperiod.link <- function(dstar) {
    structure(
        list(
            # Link
            linkfun = function(mu) {log(mu - dstar)} ,
            # Inverse link
            linkinv = function(eta) {exp(eta) + dstar} ,
            # Derivative of the inverse link (d_mu/d_eta)
            mu.eta = function(eta) {exp(eta)},
            # Functions for domain checking
            valideta = function(eta) TRUE,
            validmu = function(mu) mu > dstar ,
            name = "modperiod.link"
        ),
        class = "link-glm" 
    )
}

# Exercise 6a
# Fit the GLM
GLM.1 <- glm(
    d ~ factor(surv.int) + factor(sex) - 1, 
    offset = log(pyrs),
    family = poisson(link = modperiod.link(st.e2$d.exp)),
    data = as.data.frame(st.e2),    # From Exercise 4
    maxit = 50      # Required 4 iterations
)

# Exercise 6b
# First we need to repeat Exercise 4 but for sex and agegroup
st.e2.new <- survtab(
    Surv(time = FUT, event = lex.Xst) ~ sex + bagegroup,
    data = x,
    surv.type = "surv.rel",
    relsurv.method = "e2",
    breaks = list(FUT = seq(0, 5, 1/12), year = c(2000, 2008)),
    pophaz = popmort
)

# Fit the GLM
GLM.2 <- glm(
    d ~ factor(surv.int) + factor(bagegroup) + factor(sex) - 1, 
    offset = log(pyrs),
    family = poisson(link = modperiod.link(st.e2.new$d.exp)),
    data = as.data.frame(st.e2.new),
    maxit = 55,      # Required 51 iterations
    etastart = rep(2, nrow(as.data.frame(st.e2.new)))
)
# Exercise 7
# Linear predictor without offset
xb <- GLM.1$linear.predictors - log(GLM.1$data$pyrs)

# Interval-specific relative survival
rhat <- exp(-exp(xb)*1/12)

# Relative survival
rel.surv <- c(
    cumprod(rhat[1:60]),
    cumprod(rhat[61:120])
)

# Visualise relative survival functions
dat <- as.data.frame(st.e2)[,c(1, 3, 13:15)] 
names(dat) <- c("sex", "time", "lo", "y", "hi")
dat.glm <- dat
dat.glm$lo <- NA
# dat.glm$y <- GLM.1$fitted.values
dat.glm$y <- rel.surv
dat.glm$hi <- NA
dat <- rbind(dat, dat.glm)
dat$type <- rep(c("Unmodelled (Exercise 4)", "GLM (Exercise 6a)"), each = nrow(st.e2))

ggplot(dat, aes(x = time, y = y, colour = factor(sex), fill = factor(sex), 
        group = sex)) +
    geom_line(aes(linetype = factor(sex)), size = 1) +
    geom_ribbon(aes(ymin = lo, ymax = hi), alpha = 0.2, colour = NA) +
    labs(x = "Time from Entry", y = "Survival") +
    scale_linetype("Sex") +
    scale_fill_discrete("Sex") +
    scale_colour_discrete("Sex") +
    facet_grid( ~ type)

As expected, the survival functions are basically identical (since this GLM does not adjust for any covariates). On a practical note, there is no advantage to running an unadjusted GLM to calculate unadjusted relative survival. However, these exercises show how a GLM can be used to calculate relative survival, and extending it to include covariates is straightforward. More importantly for our purposes, an adjusted GLM provides a means of checking whether our regression estimates obtained from a Bayesian model are reasonable or not.

Note: For the purpose of visualising the survival curve, breaking up the time intervals into smaller increments is sensible. Here we have used monthly intervals, FUT = seq(0, 5, 1/12). If the goal is simply to provide estimates for each year, use FUT = seq(0, 5, 1).

Troubleshooting tips:

  • If you see the warning: glm.fit: algorithm did not converge, try increasing the maxit parameter.
  • If you see the error: cannot find valid starting values: please specify some, try adding values for the etastart parameter.

9.9.5 Fitting a Relative Survival Model: Spatial

In this example we model small-area relative survival using Bayesian methods. To obtain the input data for the model, we proceed as in the previous exercise. Once we have our cancer data and our popmort data we can calculate relative survival using the Ederer II method. The only difference is we need to have these aggregated by small areas, as well as any covariates, and also our preferred follow-up time intervals (e.g. annually). The data used corresponds to a Queensland shapefile, but for statistical local areas (SLAs) rather than the SA2s that we previously used in Chapter 7.

The following code is provided to import the simulated cancer data and the shapefile. The cancer data is modified by removing those records which have a “start” value greater than 5 years. Then the cancer data is matched against the shapefile to provide unique IDs for the areas with the values ranging from 1 to \(N\), the number of areas for which we have observed data (this is important for modelling).

The variables in this “sim survival” data set are described in Appendix B.3.

# Read in the cancer data
data <- readRDS("Downloaded Data/9.9.5 sim survival.rds")
head(data)
## # A tibble: 6 × 12
##   start   end     n     d d_star     y   sex   sla site10group bagegrp      nu  grid
##   <int> <dbl> <int> <dbl>  <dbl> <dbl> <int> <dbl>       <int>   <dbl>   <dbl> <dbl>
## 1     0     1     2     0 0.0169 1.28      1 30150          39       3 -0.0133     1
## 2     0     1     1     0 0.0328 0.572     1 30150          39       4 -0.0574     1
## 3     1     2     2     0 0.0151 1.11      1 30150          39       3 -0.0136     1
## 4     1     2     1     0 0.0581 0.591     1 30150          39       4 -0.0983     1
## 5     2     3     2     0 0.0188 1.18      1 30150          39       3 -0.0160     1
## 6     2     3     1     1 0.0387 0.372     1 30150          39       4  2.58       1
# Remove time periods after 5 years
data <- filter(data, start < 5)

# Import the shapefile
map <- st_read("Downloaded Data/Shapefile_QLD_SLA.shp") %>%
    st_make_valid()
## Reading layer `Shapefile_QLD_SLA' from data source 
##   `/home/earl/Documents/Atlas eBook/Downloaded Data/Shapefile_QLD_SLA.shp' using driver `ESRI Shapefile'
## Simple feature collection with 478 features and 5 fields
## Geometry type: MULTIPOLYGON
## Dimension:     XY
## Bounding box:  xmin: 137.996 ymin: -29.1779 xmax: 153.5522 ymax: -9.142176
## Geodetic CRS:  GRS 1980(IUGG, 1980)
N <- nrow(map)

# Create map border
map.border <- map %>% 
    select() %>%  # Ignore everything except the geometry
    summarise()  # Dissolves the SLA boundaries into one large region

The binary, first-order, adjacency matrix will be used as the spatial weights for this model, as was done previously in Section 7.3 and Section 8.3.

# Create binary, first-order, adjacency spatial weights matrix
W <- st_touches(map) %>%
    as.matrix() * 1

# Which areas have no neighbours?
no.neighbours <- which(rowSums(W) == 0)
no.neighbours
##  [1]   4  18 116 229 237 291 297 340 354 359 374 390 413 442 459 463 477 478

There are 18 areas without any first-order neighbours. We could construct artificial neighbours for these areas, as demonstrated in Section 7.3. However, we have provided a .gal file in which some links for these areas have already been added. We just need to load this file instead, and update the spatial weights.

# Create list of neighbours
nb <- spdep::read.gal("Downloaded Data/9.9.5 SLA_QLD_06_region_qv5.gal", override.id = TRUE)

# Convert to adjacency data (this is the format required by OpenBUGS)
adj.data <- spdep::nb2WB(nb)

The spatial relative survival model we consider here is exactly the same as that used in the ACA (see Section 9.8.2), except we denote the SRE by \(S\) rather than \(u\). Here is a DAG representation of the model:

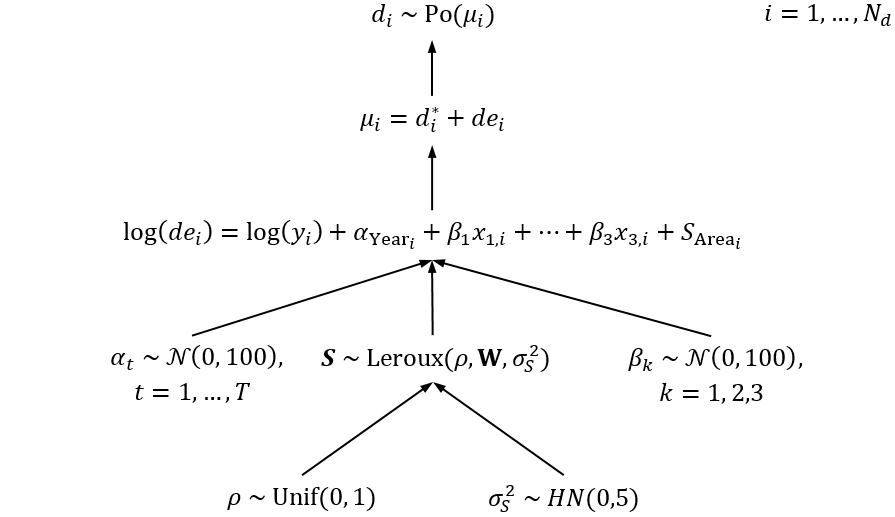
where \(i = 1, \ldots, N_d\) and \(N_d\) is the number of unit records (data rows); \(N\) is the number of areas; \(T\) is the number of follow-up years; \(d_i\) is the number of deaths in data row \(i\); \(d_i^*\) is the expected number of deaths due to causes other than the cancer of interest; \(de_i\) is the excess number of deaths; \(y_i\) is the person-time at risk; \(x_{1,i},\ldots,x_{3,i}\) are indicator variables for the three broad age groups; \({\bf W}\) is a symmetric spatial weights matrix; and \(\text{Leroux}(\rho, {\bf W}, \sigma_S^2)\) is shorthand for the Leroux prior

\[\mathcal{N}\left(\frac{\rho \sum_j{w_{hj}S_j} }{\rho \sum_j{w_{hj}}+1-\rho}, \frac{\sigma_S^2}{ \rho \sum_j{w_{hj}}+1-\rho}\right) \hspace{1em} h, j=1,\ldots,N.\]

Exercises:

  1. Translate the model specification above into OpenBUGS code and save it using write.model.
  2. Define the fixed values to be passed to OpenBUGS as data.
  3. Specify initial values for the stochastic parameters, then fit the Leroux model to the data using OpenBUGS.
  4. Summarise the posterior distributions graphically.
  5. Summarise the excess hazard ratio (EHR) graphically. (Recall the EHR is the exponentiated spatial random effect.)
# Exercise 1
# OpenBUGS spatial relative survival model
model <- function(){ 
    for(i in 1:N.d){
        d[i] ~ dpois(mu[i])
        mu[i] <- d.star[i] + d.excess[i]
        log(d.excess[i]) <- log(y[i]) + alpha[RiskYear[i]] + beta[1] * agegp2[i] + 
            beta[2] * agegp3[i] + beta[3] * agegp4[i] + S[Area[i]]
    }
    
    # Leroux prior for spatial effects
    for(j in 1:N){
        S[j] ~ dnorm(mean.S[j], prec.S[j])
        A[j] <- (rho * num[j] + 1 - rho)
        prec.S[j] <- A[j] / sigma.sq.S
        mean.S[j] <- rho * sum(W.S[cum[j] + 1:cum[j+1]]) / A[j]
    }
    
    for (h in 1:sumnum) {
        W.S[h] <- S[adj[h]]
    }
    
    # Other priors
    sigma.sq.S ~ dnorm(0, 0.2)%_%T(0,)
    rho ~ dunif(0, 1)
    
    for(t in 1:T){
        alpha[t] ~ dnorm(0, 0.01) 
    }
    
    for(k in 1:3){
        beta[k] ~ dnorm(0, 0.01)
    }
}

# Save model to a temporary location
fp.model <- file.path(tempdir(), "OpenBUGS Model 9.9.5.txt")
write.model(model, fp.model)
# Exercise 2
# Fixed values
bugs.dat <- list(
    N = N,                  # Number of areas (SLAs)
    T = 5,                  # Number of risk years
    N.d = nrow(data),       # Number of data rows
    d = data$d,             # Number of deaths
    d.star = data$d_star,   # Expected number of deaths due to other causes
    y = data$y,             # Person-time at risk offset
    RiskYear = data$start + 1,
    Area = data$grid,       # Index of areas
    adj = adj.data$adj,
    num = adj.data$num,
    cum = c(cumsum(adj.data$num) - adj.data$num, sum(adj.data$num)),
    sumnum = sum(adj.data$num),
    agegp2 = as.numeric(data$bagegrp == 2), 
    agegp3 = as.numeric(data$bagegrp == 3), 
    agegp4 = as.numeric(data$bagegrp == 4)
)
# Exercise 3
# Initial values for stochastic parameters
set.seed(1)
inits <- function() {list(
    alpha = rep(-3, 5),
    S = rep(0, N),
    sigma.sq.S = 0.2,
    rho = 0.5,
    beta = rep(0, 3)      # Coefficients for the 3 age groups
)}

# MCMC parameters
M.burnin <- 50000       # Number of burn-in iterations (discarded)
M <- 5000               # Number of iterations retained (after thinning)
n.thin <- 5             # Thinning factor
# Fit the model using OpenBUGS
MCMC <- R2OpenBUGS::bugs(
    data = bugs.dat,
    inits = inits,
    parameters.to.save = c("alpha", "beta", "S", "rho", "sigma.sq.S"),
    model.file = fp.model,
    n.chains = 1,
    n.burnin = M.burnin,
    n.iter = M.burnin + M,
    n.thin = n.thin,
    DIC = FALSE
)

# Store the list of parameters for convenience (ignore the other stuff in MCMC)
pars <- MCMC$sims.list
# Exercise 4
# Total number of sub-plots
gg.post <- vector("list", 6)

# Plot for alpha
dat <- pars$alpha
mean <- apply(dat, 2, mean)
CI.lower <- apply(dat, 2, quantile, probs = 0.025)
CI.upper <- apply(dat, 2, quantile, probs = 0.975)
dat <- data.frame(id = 1:5, mean, CI.lower, CI.upper)
gg.post[[1]] <- ggplot(dat, aes(x = id, y = mean)) + 
    geom_pointrange(aes(ymin = CI.lower, ymax = CI.upper), 
        fatten = 2, colour = "black") +
    geom_point(size = 1) +
    scale_x_continuous("Risk Year, t") +
    scale_y_continuous(expression(alpha[t])) +
    coord_flip()

# Plot for beta
dat <- pars$beta
mean <- apply(dat, 2, mean)
CI.lower <- apply(dat, 2, quantile, probs = 0.025)
CI.upper <- apply(dat, 2, quantile, probs = 0.975)
dat <- data.frame(id = 1:3, mean, CI.lower, CI.upper)
gg.post[[2]] <- ggplot(dat, aes(x = id, y = mean)) + 
    geom_pointrange(aes(ymin = CI.lower, ymax = CI.upper), 
        fatten = 2, colour = "black") +
    geom_point(size = 1) +
    scale_x_continuous("Covariate, k") +
    scale_y_continuous(expression(beta[k])) +
    coord_flip()

# Plot for S
dat <- pars$S
mean <- apply(dat, 2, mean)
CI.lower <- apply(dat, 2, quantile, probs = 0.025)
CI.upper <- apply(dat, 2, quantile, probs = 0.975)
rank <- order(order(mean))
dat <- data.frame(id = rank, mean, CI.lower, CI.upper)
gg.post[[3]] <- ggplot(dat, aes(x = id, y = mean)) + 
    geom_pointrange(aes(ymin = CI.lower, ymax = CI.upper), 
        alpha = 0.3, fatten = 0.1, colour = "grey50") +
    geom_point(size = 1) +
    scale_x_continuous("Ranked SA2", breaks = seq(0, N, 100)) +
    scale_y_continuous(expression(S)) +
    coord_flip()

# Plot for relative risk (EHR)
EHR.labels <- c(0.25, 0.5, 1, 2, 4) # Ratio scale labels
gg.post[[4]] <- ggplot(dat, aes(x = id, y = mean)) + 
    geom_pointrange(aes(ymin = CI.lower, ymax = CI.upper), 
        alpha = 0.3, fatten = 0.1, colour = "grey50") +
    geom_point(size = 1) +
    scale_x_continuous("Ranked SA2", breaks = seq(0, N, 100)) +
    scale_y_continuous("EHR", breaks = log(EHR.labels), labels = EHR.labels) +
    coord_flip(ylim = log(range(EHR.labels)))

# Plot for rho
dat <- data.frame(val = pars$rho)
gg.post[[5]] <- ggplot(dat, aes(x = val)) + 
    geom_density(fill = "black", alpha = 0.5, color = NA) +
    scale_x_continuous(expression(rho)) +
    scale_y_continuous("")

# Plot for sigma^2
dat <- data.frame(val = pars$sigma.sq.S)
gg.post[[6]] <- ggplot(dat, aes(x = val)) + 
    geom_density(fill = "black", alpha = 0.5, color = NA) +
    scale_x_continuous(expression(var[S])) +
    scale_y_continuous("")

# View combined plots
grid.arrange(
    gg.post[[1]], gg.post[[2]], gg.post[[3]], gg.post[[4]], gg.post[[5]], gg.post[[6]], 
    ncol = 3
)

# Exercise 5
# Add the EHR values to the sf object
dat <- map %>%
    mutate(
        EHR = exp(apply(pars$S, 2, median)),
        # For clarity, truncate extreme EHR values
        EHR = case_when(
            EHR > 4 ~ 4,
            EHR < 0.25 ~ 0.25,
            TRUE ~ EHR
        )
    )

# Fill colours and values for EHR
Fill.colours <- c("#2C7BB6", "#2C7BB6", "#ABD9E9", "#FFFFBF", "#FDAE61", "#D7191C", 
    "#D7191C")
Fill.values <- c(log2(1/4), seq(log2(1/1.5), log2(1.5), length = 5), log2(4))

Breaks.EHR <- c(0.5, 1/1.5, 1, 1.5, 2)

ggplot(data = dat, aes(geometry = geometry)) +
    geom_sf(data = map.border, fill = "grey30", color = "black", size = 0.8) +
    geom_sf(aes(fill = log2(EHR)), color = NA) +
    scale_fill_gradientn("",
        colours = Fill.colours, 
        values = rescale(Fill.values, na.rm = TRUE),
        limits = range(Fill.values), 
        breaks = log2(Breaks.EHR), 
        labels = round(Breaks.EHR, 3)
    ) +
    theme_void() + 
    theme(legend.position = "bottom") +
    guides(fill = guide_colourbar(barwidth = 15)) +
    ggtitle("EHR")

References

Baade, P., S. Cramb, P. Dasgupta, and D. Youlden. 2016. “Estimating cancer survival - improving accuracy and relevance.” Australian and New Zealand Journal of Public Health 40 (5): –404. https://doi.org/10.1111/1753-6405.12610.
Berkson, J. 1942. “The calculation of survival rates.” In Carcinoma and Other Malignant Lesions of the Stomach, edited by W. Walters, H. K. Gray, and J. T. Priestley, pp. 467–484. Sanders.
———. 2011b. “Developing the atlas of cancer in Queensland: methodological issues.” International Journal of Health Geographics 10 (1). https://doi.org/10.1186/1476-072x-10-9.
Cramb, S. M., K. L. Mengersen, P. C. Lambert, Ryan L. M., and P. D. Baade. 2016. “A flexible parametric approach to examining spatial variation in relative survival.” Statistics in Medicine 35 (29): –5463. https://doi.org/10.1002/sim.7071.
Cramb, S. M., K. L. Mengersen, G. Turrell, and P. D. Baade. 2012. “Spatial inequalities in colorectal and breast cancer survival: premature deaths and associated factors.” Health and Place 18 (6): –1421. https://doi.org/10.1016/j.healthplace.2012.07.006.
Dickman, P. W., P. C. Lambert, and T. Hakulinen. 2018. Population-Based Cancer Survival Analysis. Wiley.
Dickman, P. W., A. Sloggett, M. Hills, and T. Hakulinen. 2004. “Regression models for relative survival.” Statistics in Medicine 23 (1): –64. https://doi.org/10.1002/sim.1597.
Ederer, F., L. M. Axtell, and S. J. Cutler. 1961. The Relative Survival Rate: A Statistical Methodology. National Cancer Institute Monograph.
Ederer, F., and H. Heise. 1959. Instructions to IBM 650 Programmers in Processing Survival Computations. Methodological Note No. 10, End Results Evaluation Section. Technical Report. Bethesda, MD: National Cancer Institute.
Fairley, L., D. Forman, R. West, and S. Manda. 2008. “Spatial variation in prostate cancer survival in the Northern and Yorkshire region of England using Bayesian relative survival smoothing.” British Journal of Cancer 99 (11): –1793. https://doi.org/10.1038/sj.bjc.6604757.
Hakulinen, T. 1982. “Cancer survival corrected for heterogeneity in patient withdrawal.” Biometrics 38 (4). https://doi.org/10.2307/2529873.
Hennerfeind, A., L. Held, and E. A. Sauleau. 2008. “A Bayesian analysis of relative cancer survival with geoadditive models.” Statistical Modelling 8 (2): –139. https://doi.org/10.1177/1471082X0800800201.
Hinchliffe, S. R., M. J. Rutherford, M. J. Crowther, C. P. Nelson, and P. C. Lambert. 2012. “Should relative survival be used with lung cancer data?” British Journal of Cancer 106 (11): –1859. https://doi.org/10.1038/bjc.2012.182.
Holleczek, B., and H. Brenner. 2013. “Model based period analysis of absolute and relative survival with R: Data preparation, model fitting and derivation of survival estimates.” Computer Methods and Programs in Biomedicine 110 (2): –202. https://doi.org/10.1016/j.cmpb.2012.10.004.
Perme, M. P., J. Stare, and J. Estève. 2012. “On estimation in relative survival.” Biometrics 68 (1): –120. https://doi.org/10.1111/j.1541-0420.2011.01640.x.
Saez, M., M. A. Barceló, C. Martos, C. Saurina, R. Marcos-Gragera, G. Renart, R. Ocaña-Riola, C. Feja, and T. Alcalá. 2012. “Spatial variability in relative survival from female breast cancer.” Journal of the Royal Statistical Society: Series A (Statistics in Society) 175 (1): –134. https://doi.org/10.1111/j.1467-985x.2011.00720.x.

  1. Originally written for WinBUGS, the predecessor to OpenBUGS. No change to the model is required to run in OpenBUGS.↩︎

  2. This model was also run using WinBUGS originally. To run in OpenBUGS, the truncation I(0,) was changed to T(0,) for parameter sigma.s2.↩︎