Appendix A: Worked Examples
A.1: Bayes Theorem Example 1: Probability Tree Diagram
This example is adapted from Berry and D. K. Stangl (eds) (1996).
Consider a diagnostic test for cancer. The test can signal either positive (+) or negative (-) diagnosis. Let \(C\) and \(\bar{C}\) denote that someone has or does not have cancer respectively. Suppose the cancer is rare, with \(\text{Pr}(C)=0.001\), and the diagnostic test is quite accurate, with sensitivity \(\text{Pr}(+|C)=0.9\) and specificity \(\text{Pr}(-|\bar{C})=0.95\).
Exercises:
- Draw a tree diagram showing the 4 possible outcomes and the corresponding probabilities.
- If a patient receives a positive diagnosis, what is the chance that they actually have cancer? That is, determine \(\text{Pr}(C|+)\).
- Suppose that the cancer is more common with \(\text{Pr}(C)=0.1\). Now what is the chance that a patient with a positive diagnosis actually has cancer?
Solutions:
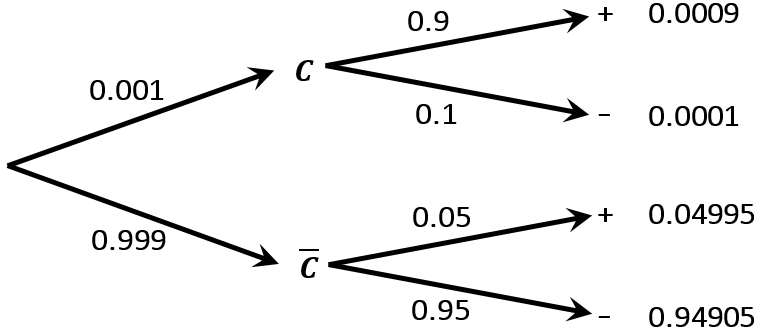
Using Bayes theorem and the probabilities from the tree diagram:
\[\begin{align*} \text{Pr}(C|+) = & \frac{\text{Pr}(+|C)\text{Pr}(C)}{\text{Pr}(+)} \\ = & \frac{\text{Pr}(+|C)\text{Pr}(C)}{\text{Pr}(+|C)\text{Pr}(C) + \text{Pr}(+|\bar{C})\text{Pr}\bar{C}} \\ = & \frac{0.9 \times 0.001}{0.9(0.001) + 0.05(0.999)} \\ = & \frac{0.0009}{0.05085} \\ \approx & 0.0177 \end{align*}\]
So even though this test is accurate (high sensitivity), the patient who tests positive has less than a 2% chance of actually having cancer. This is because the cancer is rare which is reflected by the prior probability of having cancer \(\text{Pr}(C)\) being small. In other words, the prior probability is having a strong influence on the posterior probability.
Using Bayes theorem again:
\[\begin{align*} \text{Pr}(C|+) = & \frac{\text{Pr}(+|C)\text{Pr}(C)}{\text{Pr}(+)} \\ = & \frac{\text{Pr}(+|C)\text{Pr}(C)}{\text{Pr}(+|C)\text{Pr}(C) + \text{Pr}(+|\bar{C})\text{Pr}\bar{C}} \\ = & \frac{0.9 \times 0.1}{0.9(0.1) + 0.05(0.9)} \\ = & \frac{0.09}{0.135} \\ \approx & 0.6667 \end{align*}\]
In this scenario, when cancer is common, the patient with a positive test result has about a 67% chance of actually having cancer.
A.2: Bayes Theorem Example 2: Beta-binomial model
Suppose we wish to learn about the incidence of a particular disease in the population. Further suppose that medical records show that out of a sample of 53 patients, only 4 had the disease of interest.
Exercises:
- Assuming a beta distribution for the prior, determine the unnormalised posterior distribution in analytical form using Bayes’ theorem.
- Determine the marginal distribution of \(y\) and use it to obtain the normalised posterior.
- Plot the posterior using the observed data and:
- beta distribution with shape parameters (1, 1) (a flat prior); and
- beta distribution with shape parameters (1, 20).
Solutions:
Here the unknown parameter is the incidence, denoted \(\theta\). The data \(y\) represent a sample from a binomial experiment (each hospital record is a trial, with only two possible outcomes: disease (success) or no disease (failure)), so the likelihood is binomial:
\[\begin{align*} p(y|\theta) = & \text{Bin}(y|n, \theta) \\ = & \binom{n}{y}\theta^y (1-\theta)^{n-y} \hspace{1em} \text{where } n=53 \text{ trials} \end{align*}\]
And the distribution for the prior is a beta distribution:
\[\begin{align*} p(\theta) = & \text{Beta}(\theta|\alpha, \beta) \\ = & \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{\text{B}(\alpha, \beta)} \end{align*}\]
So, using Bayes’ theorem:
\[\begin{align*} p(\theta|y) \propto & p(y|\theta)p(\theta) \\ = & \binom{n}{y}\theta^y (1-\theta)^{n-y} \frac{\theta^{\alpha-1}(1-\theta)^{\beta-1}}{\text{B}(\alpha, \beta)} \\ = & \binom{n}{y} \frac{\theta^{y+\alpha-1}(1-\theta)^{n-y+\beta-1}}{\text{B}(\alpha, \beta)} \\ \propto & \theta^{y+\alpha-1}(1-\theta)^{n-y+\beta-1} \end{align*}\]
where \(y\), \(\alpha\), \(\beta\), and \(n\) are all (assumed) known a priori, i.e. they are not unknown parameters but fixed; \(\theta\) is the only unknown parameter.
To determine the marginal distribution of \(y\), we need to integrate the unnormalised posterior distribution:
\[\begin{align*} p(y) = & \int{p(y|\theta)p(\theta)d\theta} \\ = & \binom{n}{y} \frac{1}{\text{B}(\alpha, \beta)} \int{\theta^{y+\alpha-1}(1-\theta)^{n-y+\beta-1}d\theta} \end{align*}\]
Now, we could simply expand the integrand and perform the integration, but we would end up with an expression which isn’t very helpful. Instead we can use the identity,
\[ \text{B}(a, b) = \int_0^1{t^{a-1}(1-t)^{b-1}dt} \]
so
\[ p(y) = \binom{n}{y}\frac{1}{\text{B}(\alpha, \beta)} \text{B}(y+\alpha, n-y+\beta) \]
(which is the beta-binomial distribution). Therefore, the normalised posterior is:
\[\begin{align*} p(\theta|y) = & \frac{p(y|\theta)p(\theta)}{p(y)} \\ = & \frac{\binom{n}{y} \frac{1}{\text{B}(\alpha, \beta)}\theta^{y+\alpha-1}(1-\theta)^{n-y+\beta-1}}{\binom{n}{y}\frac{1}{\text{B}(\alpha, \beta)} \text{B}(y+\alpha, n-y+\beta)} \\ = & \frac{\theta^{y+\alpha-1}(1-\theta)^{n-y+\beta-1}}{\text{B}(y+\alpha, n-y+\beta)} \\ = & \text{Beta}(\theta | y+\alpha, n-y+\beta) \end{align*}\]
That is, the posterior is also a beta distribution, with shape parameters \(y+\alpha\) and \(n-y+\beta\). The reason that the posterior has the same form as the prior (both beta distributions, different parameters) is because the beta distribution is a conjugate prior to the binomial distribution. When a conjugate prior is used, the posterior has the same form. Using conjugate priors can make calculations easier to do by hand, and even offer some computational gains in real-world problems, but they are not crucial to use in practice.
Note that in this example, we could have determined the posterior was a beta distribution without integrating the marginal distribution of \(y\) over \(\theta\) for two reasons: 1) because the prior was conjugate, and 2) because we can compare the form of the unormalised posterior \(\theta^{y+\alpha-1} (1-\theta)^{n-y+\beta-1}\) with a beta distribution and observe that they match. (In general, if the prior is not conjugate and the unormalised posterior cannot be matched to a recognisable distribution, then integrating the marginal distribution would be necessary to determine the analytical form of the posterior. But we reiterate that this is almost always impossible in practice, and also totally unnecessary.)
Plotting the posterior:
\[\begin{align*} p(\theta|y)_1 = & \text{Beta}(\theta | 4 + 1, 53-4+1) \\ = & \text{Beta}(\theta | 5, 50) \end{align*}\]
\[\begin{align*} p(\theta|y)_2 = & \text{Beta}(\theta | 4 + 1, 53-4+20) \\ = & \text{Beta}(\theta | 5, 69) \end{align*}\]
x <- seq(0, 1, 0.005)
dat <- data.frame(
x = rep(x, 2),
y = c(
dbeta(x, shape1 = 5, shape2 = 50),
dbeta(x, shape1 = 5, shape2 = 69)
),
group = rep(1:2, each = length(x))
)
ggplot(dat, aes(x = x, y = y, color = factor(group))) +
geom_line(size = 1, alpha = 0.6) +
scale_color_discrete("", labels = c("beta(5, 50)", "beta(5, 69)")) +
guides(color = guide_legend(override.aes = list(alpha = 1)))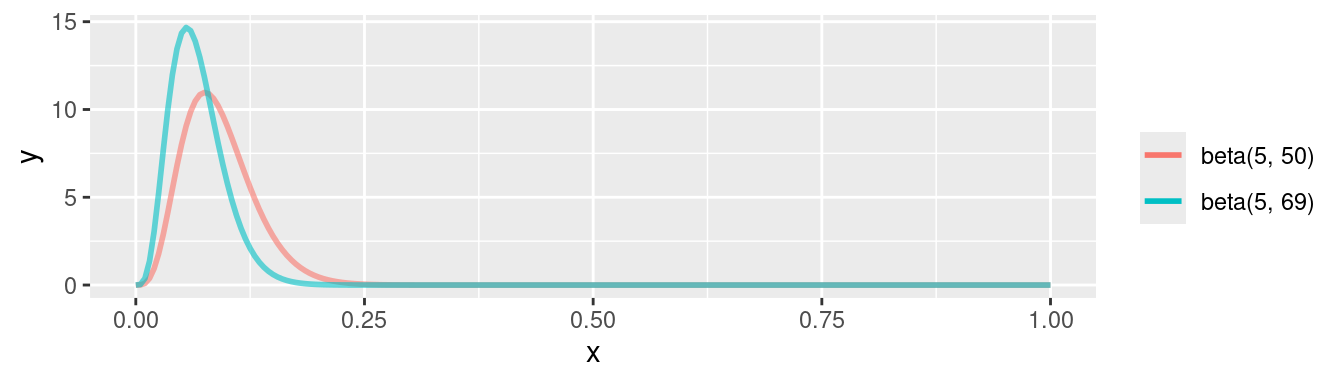
A.3: OpenBUGS Example
Models can be implemented in OpenBUGS directly from R. We illustrate how to use the R package R2OpenBUGS (Sturtz, Ligges, and Gelman 2010) to implement a simple example problem, taken from the WinBUGS/OpenBUGS help files. (The file can be found online here.
The model is as follows:
\[ x_i \sim \text{Poisson}(\theta_i t_i) \\ \theta_i \sim \text{Gamma}(\alpha, \beta) \\ \alpha \sim \text{Exp}(1) \\ \beta \sim \text{Gamma}(0.1, 1) \]
for \(i=1,\ldots,10\) where \(\theta_i\) is the failure rate, and \(t_i\) is the total amount of time that the \(i^{\text{th}}\) pump has been in operation (measured) in 1000s of hours. Please refer to the link above for more details. The following code demonstrates the process of creating the model and other information required by OpenBUGS to execute properly.
First, we translate the model specification above into a script that can be read by OpenBUGS. The model is then saved as a text file. Optionally, this file can be viewed using file.show().
Note the code between function(){ and the corresponding closing } is OpenBUGS syntax, which is conveniently very similar to R syntax, but has some important nuances. For example:
- Distributions are specified using the letter “d” followed by the [abbreviated] density name, rather than the letter “r”. E.g. draws from the Poisson distribution are denoted by
dpoisrather thanrpois. - The Gaussian distribution is parameterised in terms of mean and precision (inverse variance) rather than mean and standard deviation as in R.
- Operations are not permitted inside functions, including distributions. E.g.
log(beta + 1) <- alphais invalid, but the mathematically equivalentbeta <- exp(alpha) - 1is valid. Alternatively, an intermediate dummy variable can be used, e.g.log(tmp) <- alphawithbeta <- tmp - 1. Note the use of the dummy variable in the code below for the product \(\theta_i t_i\). - Truncation is specified using the
T()function, e.g.dnorm(mu,tau)T(low, high). One-sided truncation is specified by omitting one of the limits. When including thisT()function in a model script written usingwrite.model, the dummy operator%_%must be inserted, e.g.dnorm(mu,tau)%_%T(low, high)(see Section 8.3 and Exercise 1 in Section 9.9.5). TheT()function can also be used to specify folded prior distributions like the half-Normal distribution. However, care must be taken to ensure that the normalising constant does not depend on any unknown parameters, otherwise the resulting distribution will be incorrect (see D. Spiegelhalter et al. (2003), pp. 14 and D. Lunn et al. (2012), ch. 9). (Unlike WinBUGS, OpenBUGS also has an explicit function for censoring, namelyC().)
library(R2OpenBUGS)
# The model
model.pump <- function(){
for (i in 1:N) {
x[i] ~ dpois(tmp[i])
tmp[i] <- theta[i] * t[i] # Deterministic node explicit
theta[i] ~ dgamma(alpha, beta)
}
alpha ~ dexp(1)
beta ~ dgamma(0.1, 1.0)
}
# Save model as "text" file in temporary location
fp.model <- file.path(tempdir(), "pump_example.txt")
write.model(model.pump, fp.model)
# View model (optional)
file.show(fp.model)Next, we create a list of all the values in the model file which are fixed. This includes the variables which are measured, \(t\), variables which are observed, \(x\), and the sample size, \(N\), which determines the number of iterations of the for loop.
# Fixed values as a named list
data.pump <- list(
t = c(94.3, 15.7, 62.9, 126, 5.24, 31.4, 1.05, 1.05, 2.1, 10.5),
x = c( 5, 1, 5, 14, 3, 19, 1, 1, 4, 22),
N = 10
)We also need to specify a list of initial values for the parameters in the model file which are stochastic, that is, which must be estimated. Essentially, this is all the parameters which have a distribution except those which are observed (in this case, \(x\)).
# Initial values for stochastic parameters
inits.pump <- function() {list(
theta = rgamma(10, 1, 1),
alpha = 1,
beta = 1
)}Lastly, we specify the length of the burn-in and the posterior sample size, then run the model using bugs() which calls OpenBUGS to run in the background. If everything has been specified correctly, OpenBUGS will begin to estimate the posterior. Once complete, the results are automatically returned to R and assigned to the object specified by the user, here Pump.example.
# MCMC parameters
M.burnin <- 1000 # Number of burn-in iterations (discarded)
M <- 10000 # Number of iterations retained
# Fit the model using OpenBUGS
set.seed(1)
Pump.example <- bugs(
data = data.pump,
inits = inits.pump,
parameters.to.save = c("theta", "alpha", "beta"),
model.file = fp.model,
n.chains = 1,
n.burnin = M.burnin,
n.iter = M.burnin + M, # Total iterations
n.thin = 1,
DIC = FALSE
)Using the print() function on the object Pump.example gives a tabular summary of the posterior estimates for each parameter.
## Inference for Bugs model at "/tmp/RtmpSiiQwK/pump_example.txt",
## Current: 1 chains, each with 11000 iterations (first 1000 discarded)
## Cumulative: n.sims = 10000 iterations saved
## mean sd 2.5% 25% 50% 75% 97.5%
## theta[1] 0.1 0.0 0.0 0.0 0.1 0.1 0.1
## theta[2] 0.1 0.1 0.0 0.0 0.1 0.1 0.3
## theta[3] 0.1 0.0 0.0 0.1 0.1 0.1 0.2
## theta[4] 0.1 0.0 0.1 0.1 0.1 0.1 0.2
## theta[5] 0.6 0.3 0.2 0.4 0.5 0.8 1.3
## theta[6] 0.6 0.1 0.4 0.5 0.6 0.7 0.9
## theta[7] 0.9 0.7 0.1 0.4 0.7 1.2 2.8
## theta[8] 0.9 0.7 0.1 0.4 0.7 1.2 2.8
## theta[9] 1.6 0.8 0.5 1.0 1.4 2.0 3.4
## theta[10] 2.0 0.4 1.2 1.7 2.0 2.3 2.9
## alpha 0.7 0.3 0.3 0.5 0.7 0.9 1.3
## beta 0.9 0.5 0.2 0.5 0.8 1.2 2.2Section 3.4 contains further details on summarising the posterior and making Bayesian inference.
Appendix B: Data Dictionaries
B.1: Data Dictionaries for the Worked Example in Section 9.9.3
These three data files were originally obtained from http://www.pauldickman.com/survival/. They have been reformatted slightly and converted to the more R friendly .rds format.
Data Dictionary for the “popmort” Data File
| Variable | Value |
|---|---|
| sex | Male, Female. |
| year | Year (ranges from 1951-2000). |
| age | Age in years (ranges from 0 to 105). |
| prob | Probability of surviving 1 year. |
| haz | Mortality rate (rate = \(-\ln(prob)\)). |
Data Dictionary for the “colon” Data Set
This data set comprises 15564 records: unit-record file data of colon cancer diagnoses during 1975-1994, followed up to 1995.
| Variable | Value |
|---|---|
| sex | Male, Female. |
| AGE | Age at diagnosis (years, ranges from 0 to 99). |
| stage | Clinical stage at diagnosis (0 = unknown, 1 = localised, 2 = regional, 3 = distant). |
| mmdx | Month of diagnosis. |
| yydx | Year of diagnosis (ranges from 1975 to 1994). |
| surv_mm | Survival time in months (range: 0.5 to 251.5). |
| surv_yy | Survival time in years (range: 0.5 to 20.5). |
| status | Vital status at exit (0 = Alive, 1 = Cancer death, 2 = Other death, 4 = Lost to follow-up). |
| subsite | Anatomical subsite of tumour (1 = Caecum and ascending colon, 2 = Transverse colon, 3 = Descending and sigmoid colon, 4 = Other and NOS). |
| year8594 | Indicator for diagnosis time period (0 = 1975-1984, 1 = 1985-1994). |
| agegrp | Age group in 4 categories (0 = 0-44, 1 = 45-59, 2 = 60-74, 3 = 75+). |
| dx | Date of diagnosis (numeric code). |
| exit | Date of exit (numeric code). |
| id | Unique patient identifier. |
Data Dictionary for the “melanoma” Data Set
This data set comprises 7775 records: unit-record file data of skin melanoma diagnoses during 1975-1994, followed up to 1995.
| Variable | Value |
|---|---|
| sex | Male, Female. |
| age | Age at diagnosis (years, ranges from 0 to 99). |
| stage | Clinical stage at diagnosis (0 = unknown, 1 = localised, 2 = regional, 3 = distant). |
| mmdx | Month of diagnosis. |
| yydx | Year of diagnosis (ranges from 1975 to 1994). |
| surv_mm | Survival time in months (range: 0.5 to 251.5). |
| surv_yy | Survival time in years (range: 0.5 to 20.5). |
| status | Vital status at exit (0 = Alive, 1 = Cancer death, 2 = Other death, 4 = Lost to follow-up). |
| subsite | Anatomical subsite of tumour (1 = head and neck, 2 = Trunk, 3 = Limbs, 4 = Multiple and NOS). |
| year8594 | Indicator for diagnosis time period (0 = 1975-1984, 1 = 1985-1994). |
| dx | Date of diagnosis (numeric code). |
| exit | Date of exit (numeric code). |
| agegrp | Age group in 4 categories (0 = 0-44, 1 = 45-59, 2 = 60-74, 3 = 75+). |
| id | Unique patient identifier. |
B.2: Data Dictionaries for the Worked Example in Section 9.9.4
Data Dictionary for the “popmort” Data File
| Variable | Value |
|---|---|
| year | Ranges from 1997 to 2007. |
| sex | Male, Female. |
| agegroup | Values from 1 to 19 representing 5-year age groups (0-4, 5-9, …, 90+). |
| grid | Represents the geographical area of residence at diagnosis (values 1 to 478). |
| count | Number of deaths (all causes). |
| pop | Population size. |
Data Dictionary for the “cancer” Data Set
This data set comprises 15051 records: unit-record file data.
| Variable | Value |
|---|---|
| id | Unique identifier for each case. |
| sex | Male, Female. |
| year | Year of diagnosis. Ranges from 1997 to 2007. |
| site10group | All values are 1 (hypothetical cancer). |
| death | 0 = Alive/censored, 1 = Dead |
| age | Age at diagnosis (years). |
| bagegroup | Broad age group at diagnosis (1 = 0-49 years, 2 = 50-69 years, 3 = 70-89 years). Missing means age was 90+ years. |
| grid | Represents the geographical area of residence at diagnosis (values 1 to 478). |
| fu_date | Date of censoring (31 Dec 2007) or date of death (DDMMMYYYY), as a string. |
| exit | Same as fu_date (DDMMMYYYY). |
| dx_date | Date of diagnosis (DDMMMYYYY). |
| dth_date | Date of death (DDMMMYYYY). |
| exit_ | Numeric code for exit date. |
| surv | Time between diagnosis and censoring/death in days. |
| basis | Basis of diagnosis (1 = clinical only, 2 = clinical investigation without a tissue diagnosis, 4 = specific tumour markers, 5 = cytology, 6 = histology of metastasis, 7 = histology of a primary tumour, 8 = histology unspecified, 9 = unknown, 10 = death certificate only (DCO)) |
B.3: Data Dictionaries for the Worked Example in Section 9.9.5
Data Dictionary for the “sim survival” Data File
This data set comprises 13893 records: aggregated simulated survival estimates for model input.
| Variable | Value |
|---|---|
| start | Start of the follow-up time interval. |
| end | End of the follow-up time interval. |
| n | Number alive at the start of the interval. |
| d | Deaths during the interval. |
| d_star | Expected number of deaths \((d^*)\). |
| y | Person-time at risk |
| sex | All values are 1 (one sex). |
| sla | Statistical Local Area (SLA) of residence at diagnosis. There are 478 SLAs with values ranging from 150 to 7600. |
| site10group | All values are 39 (hypothetical cancer). |
| bagegrp | Broad age group at diagnosis (1 = 15-54 years, 2 = 55-64 years, 3 = 65-74 years, 4 = 75-89 years). Missing means age was 90+ years. |
| nu | Estimated excess mortality rate, i.e. \((d-d^*)/y\) |
| grid | Represents the SLA (consecutively numbered values 1 to 478). |