Chapter 3 Overview of Bayesian Statistical Modelling and Computation
3.1 Bayes’ Theorem
Consider the problem of estimating an unknown parameter, \(\bm{\theta}\), given some observed data, \(\bm{y}\). Note that \(\bm{\theta}\) could be either a scalar or a vector, but we use the bold font to denote the more general case that it is a vector. As an example, perhaps you are interested in estimating an unknown population mean (height, income, age, etc.). Suppose you are able to acquire a sample of \(N\) measurements from the population of interest, \(\bm{y} = \left\{y_1, y_2, \ldots, y_N\right\}\). The idea of Bayesian inference is to ask the question, “What can we learn about \(\bm{\theta}\) given that we have observed \(\bm{y}\)?” In general, the Bayesian solution consists of the following steps:
- Formalise our uncertainty of the unknown parameter(s) \(\bm{\theta}\) through a prior distribution(s), denoted \(p(\bm{\theta})\)
- Assume a reasonable distribution for the sampling distribution of \(\bm{y}\) given \(\bm{\theta}\), denoted \(p(\bm{y}|\bm{\theta})\).
- Update our knowledge about the unknown parameter(s) by computing the posterior distribution, \(p(\bm{\theta}|\bm{y})\).
This last step is achieved by applying Bayes’ theorem (Banerjee, Carlin, and Gelfand 2014):
\[ p(\bm{\theta}|\bm{y}) = \frac{p(\bm{y}|\bm{\theta})p(\bm{\theta})}{p(\bm{y})} \]
where \(p(\bm{y})\) is the marginal distribution of \(\bm{y}\), given by
\[ p(\bm{y}) = \int{p(\bm{y}|\bm{\theta})p(\bm{\theta})}d\bm{\theta} \]
Since \(p(\bm{y})\) does not depend on the unknown parameters \(\bm{\theta}\), it is regarded as a constant (called the normalising constant) as far as Bayes’ theorem is concerned, and therefore this equation simplifies to:
\[ p(\bm{y}) \propto p(\bm{y}|\bm{\theta})p(\bm{\theta}) \]
The result is an unnormalised posterior distribution. However, once this distribution has been estimated, it is trivial to rescale it so that the probabilities sum to 1 (or equivalently the density integrates to 1). (In practice, this rescaling occurs automatically, since a random sample from a density will be the same whether it is normalised or not.)
Note that \(p(\bm{y}|\bm{\theta})\) is often referred to as the likelihood function. Technically, the likelihood is a function of \(\bm{\theta}\) for fixed \(\bm{y}\), say \(L(\bm{\theta}|\bm{y})\). However, the likelihood is proportional to the sampling distribution, i.e. \(L(\bm{\theta}|\bm{y}) \propto p(\bm{y}|\bm{\theta})\), so the distinction is unimportant for the task of deriving the unnormalised posterior.
Bayes’s theorem originally applied to point probabilities, that is, where \(p(\cdot)\) referred to a probability (a number) rather than a distribution, as illustrated in the worked example in Appendix A.1. But the theorem applies equally to probability distributions (densities) as demonstrated in Appendix A.2.
3.2 Marginal Posterior Distributions and Full Conditionals
In real-world problems, there are typically many unknown parameters. The prior distributions assigned to them depends on where these parameters are situated with respect to the model hierarchy. For example, the parameters may be independent of all other parameters, e.g. \(p(\theta_h)\), dependent on some parameters but conditionally independent of others, e.g. \(p(\theta_h | \theta_j)\), or co-dependent, e.g. multivariate parameters which are specified jointly \(p(\bm\theta = \{\theta_1, \theta_2, \theta_3\}|\cdot)\). Because of the [conditional] independence between the parameters, the prior for all parameters can be expressed as the factorisation of these marginal priors:
\[ p(\bm{\theta}) = p(\theta_1 | \bm{\theta}_{\setminus 1})p(\theta_2 | \bm{\theta}_{\setminus 2}) \ldots p(\theta_H | \bm{\theta}_{\setminus H}) \] where the dependence implied by \(p(\theta_h | \bm{\theta}_{\setminus h})\) can usually be greatly simplified (the subscript in \(\bm{\theta}_{\setminus h}\) denotes “all other parameters excluding \(h\)”). The resulting posterior is given by
\[ p(\bm{\theta}|\bm{y}) = p(\bm{y}|\bm{\theta})p(\bm{\theta}) = p(\theta_1 | \bm{\theta}_{\setminus 1})p(\theta_2 | \bm{\theta}_{\setminus 2}) \ldots p(\theta_H | \bm{\theta}_{\setminus H}) \]
where \(H\) is the total number of parameters (including hyper-parameters) in the model. Because of the high dimensional parameter space (the “curse of dimensionality”), it is easier to make inferences about each of the parameters by simplifying the posterior into the respective marginal posterior distributions, which are found by integrating out all the other unknown parameters. E.g. the marginal posterior for \(\theta_h\) is given by
\[\begin{align*} p(\theta_h | \bm{y}) = & \int \cdots \int{p(\theta_1, \ldots,\theta_h,\ldots,\theta_H|\bm{y})d\bm{\theta}_{\setminus h}} \\ = & \int \cdots \int{p(\theta_h | \bm{\theta}_{\setminus h},\bm{y})p(\bm{\theta}_{\setminus h}|\bm{y})d\bm{\theta}_{\setminus h}} \end{align*}\]
using the joint probability rule \(p(A, B) = p(A|B)p(B)\).
In practice, due to the complex, hierarchical structure of the model (and large number of parameters), the integration necessary to acquire the marginal posteriors is impossible. In such cases, the posterior distribution is said to be intractable.
However, in very simple cases (e.g. \(H=1\)), it is possible to calculate the posterior distribution exactly. This is demonstrated in the worked example provided in Appendix A.2.
The terms \(p(\theta_h|\bm{\theta}_{\setminus h}, \bm{y})\) for \(h = 1,\ldots,H\) are called the full conditional posterior distributions, or simply “full conditionals”. Assuming that there was a true value for each of the unknown parameters, then using plug-in estimates that approach those true values for the parameters \(\bm{\theta}_{\setminus h}\) would mean that the full conditional \(p(\theta_h|\bm{\theta}_{\setminus h}, \bm{y})\) asymptotically approaches the marginal posterior \(p(\theta_h|\bm{y})\). This is the fundamental basis of Bayesian estimation: try to find better and better estimates of the unknown parameters (often via simulation) so that the full conditionals converge to the marginal posteriors. (In reality, most unknown parameters do not have a single “true value”, but rather a plausible range of values, and this is reflected by the posterior distribution.) The resulting simulated values will come from the joint posterior distribution \(p(\bm{\theta}|\bm{y})\) as required.
3.2.1 Deriving the Full Conditionals
For most Bayesian modelling software (see Section 3.3.4), deriving the full conditionals explicitly is not required - the software automatically determines them (or approximations of them) from the likelihood and prior distributions specified by the user. However, sometimes the available software may not implement a particular model or places too many unwanted constraints on one or more parameters. In such cases, it may be necessary or preferable to implement a sampling technique by coding it from scratch. This requires deriving the full conditionals explicitly.
Deriving the analytical form of the full conditionals is usually quite straightforward. Consider the following toy example model:
\[ \bm{y}|\eta \sim \text{Poisson}(\eta) \\ \eta | \alpha, \beta \sim Gamma(\alpha, \beta) \\ \alpha \sim HN(0, 10) \\ \beta \sim \mathcal{IG}(0.5, 0.05) \] where \(HN(\cdot)\) denotes a half-Normal distribution, and \(\mathcal{IG}(\cdot)\) denotes an inverse-gamma distribution. It is helpful to create a directed acyclic graph (DAG) or similar model schematic showing the hierarchical structure of the model. E.g.
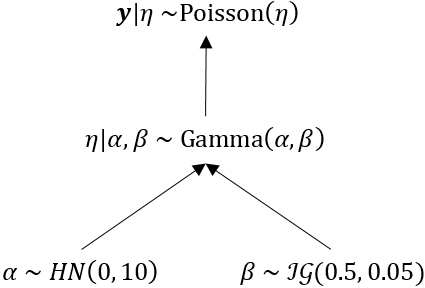
The full conditional for a given node (parameter) is simply the product of the probability model (likelihood or prior) for that node and its parent node (at least up to a constant of proportionality). E.g.
\[ p(\eta | \bm{y}, \alpha, \beta) \propto p(\eta | \alpha, \beta) \times p(\bm{y} | \eta) \\ p(\alpha | \eta, \beta) \propto p(\alpha) \times p(\eta | \alpha, \beta)\\ p(\beta | \eta, \alpha) \propto p(\beta) \times p(\eta | \alpha, \beta) \]
Note that the dependence on \(y\) for the parameters \(\alpha\) and \(\beta\) can be dropped since they are conditionally independent (they only depend on \(y\) indirectly through \(\eta\)). All that remains now is to substitute in the analytical forms of the terms on the right hand side and simplify the expressions. E.g., assuming a sample size of \(N\), the full conditional for \(\eta\) is
\[\begin{align*} p(\eta | \bm{y}, \alpha, \beta) \propto & p(\eta | \alpha, \beta) \times p(\bm{y} | \eta)\\ = & \text{Gamma}(\eta;\alpha, \beta) \times \text{Poisson}(\bm{y}; \eta) \\ = & \frac{\beta^\alpha}{\Gamma(\alpha)}\eta^{\alpha-1}e^{-\beta \eta} \prod_{i=1}^N \frac{\eta^{y_i}e^{-\eta}}{y_i!} \\ \propto & \eta^{\alpha-1}e^{-\beta \eta} \eta^{\sum_{i=1}y_i} e^{-N\eta} \\ = & \eta^{\sum_{i=1}y_i +\alpha-1}e^{-\eta(\beta + N)} \\ = & \text{Gamma}\left(\eta; \alpha + \sum_{i=1} y_i, \beta+N \right) \end{align*}\]
Like the example given in Appendix A.2, we end up with a posterior which has the same form as the prior because the gamma prior is a conjugate prior for the Poisson distribution. To obtain the marginal posterior distribution for \(\eta\), we just need good estimates of \(\alpha\) and \(\beta\). Here is an example of the marginal posterior for \(\eta\) for three different combinations of plug-in estimates of parameters \(\alpha\) and \(\beta\):
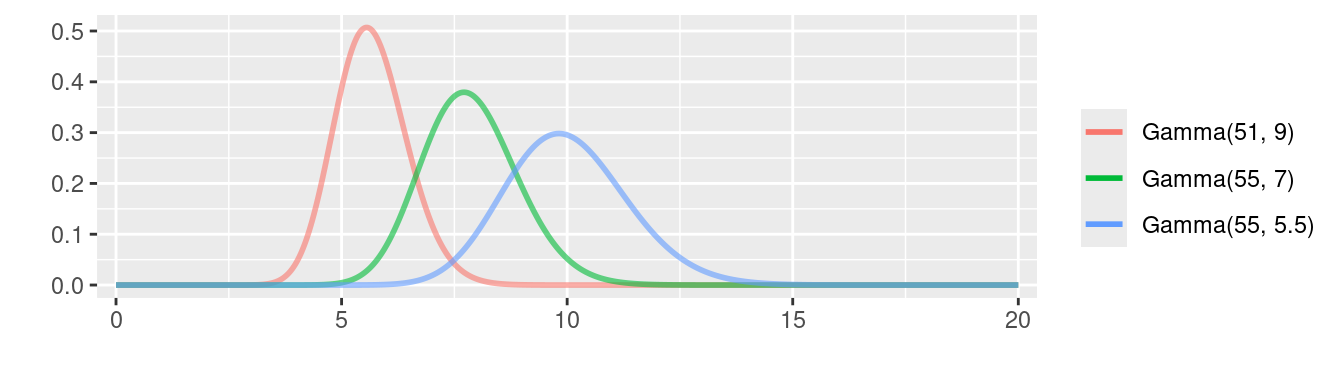
As this figure demonstrates, the marginal posterior distribution can vary quite substantially, depending on the values of the other unknown parameters that define it. This has two important ramifications:
- The prior needs to be chosen carefully so as to avoid undue influence on the posterior (see the example in Appendix A.1). This tends to be more problematic for informative priors that are misguided, leading to a contradiction of prior and posterior beliefs, but priors that are too vague can also yield poor estimates or make convergence slow.
- To obtain an accurate estimate of the marginal posterior distribution, we need accurate estimates of the unknown parameters defining it. Except for very simple models, the full conditionals will be dependent on one or more unknown parameters. In order to solve the complex interdependencies between all the unknown parameters, they need to be estimated iteratively.
3.3 Bayesian Estimation Techniques
The task of estimating the unknown parameters is a significant component of the Bayesian methodology. The techniques that are available largely depend on the properties of the full conditional distributions.
3.3.1 Monte Carlo Methods
Monte Carlo sampling methods provide a sample of independent and identically distributed (i.i.d.) draws from a distribution, given fixed inputs for any parameters defining that distribution. Consider the example from Section 3.2.1. The full conditional for \(\eta\) is a gamma distribution,
\[p(\eta|\bm{y}, \alpha, \beta) \propto \text{Gamma}\left(\eta; \alpha + \sum_{i=1} y_i, \beta+N \right).\]
For fixed (i.e. assumed known) values of \(\alpha\) and \(\beta\) (\(N\) is the sample size), we can obtain a sample from this distribution using Monte Carlo methods. This is true for most well-known distributions that we are familiar with, e.g. Normal, Poisson, gamma, exponential, binomial, etc. Most software has efficient, built-in sampling methods to achieve this. For example, we can generate random variates from these distributions in R (R Core Team 2018) using the functions rnorm, rpois, rgamma, rexp, rbinom, etc. These functions mostly involve C implementations of very low level algorithms. However, at the core of these functions is one of a variety of approaches, including inverse transformations, accept-reject sampling, taking advantage of special properties of the distribution (e.g. recognising the Binomial variate is a sum of independent Bernoulli variates), other algorithms, or a combination of these. These approaches are examples of Monte Carlo sampling. The basic idea of Monte Carlo sampling is to repeatedly sample (possibly involving some transformation functions) so that the resulting sample represents i.i.d. draws from the desired distribution.
Consider the simple example of drawing values from an exponential distribution, \(\text{Exp}(\lambda)\). There is a well-known relationship between the exponential and standard uniform distributions, namely if \(u \sim \text{Unif}(0,1)\) then \(x=-\log(u)/\lambda\) is equivalent to drawing \(x \sim \text{Exp}(\lambda)\). So the Monte Carlo method is to take repeated samples from the standard uniform distribution and transform them to yield an i.i.d. sample from the exponential distribution. This relationship between the two distributions is just a specific example of a more general approach known as the inverse cumulative density function (CDF) method.
Another popular Monte Carlo approach is accept-reject sampling. The idea is to sample from another distribution, call the proposal distribution, which is easy to sample from (e.g. a uniform or Normal distribution), such that a constant multiple of the proposal distribution envelopes the target distribution, i.e. the full conditional. That is, specify a proposal distribution \(g(x)\) such that \(c\cdot g(x)\) envelopes the full conditional \(f(x)\) for some constant \(c\), where \(g(x)\) is a probability density function which is easy to sample from directly. A sample of candidate values \(\hat{x}=(\hat{x}_1, \hat{x}_2, \ldots)\) are drawn from \(g(x)\), and a sample of auxiliary variates \(\hat{u}=(\hat{u}_1, \hat{u}_2, \ldots)\) are drawn uniformly at random from the interval \([0,c \cdot g(\hat{x})\)]. The \(i^{\text{th}}\) candidate \(\hat{x}_i\) is accepted if \(\hat{u}_i\leq f(\hat{x}_i)\), otherwise \(\hat{x}_i\) is rejected. The resulting sample represents a homogenous sample of points under the proposal distribution: the points that also lie under the target distribution are accepted; the remainder in between the proposal and target distributions are rejected. The following illustrates a sample generated using accept-reject sampling for a bimodal target distribution using Normal and uniform densities as the proposal distribution.
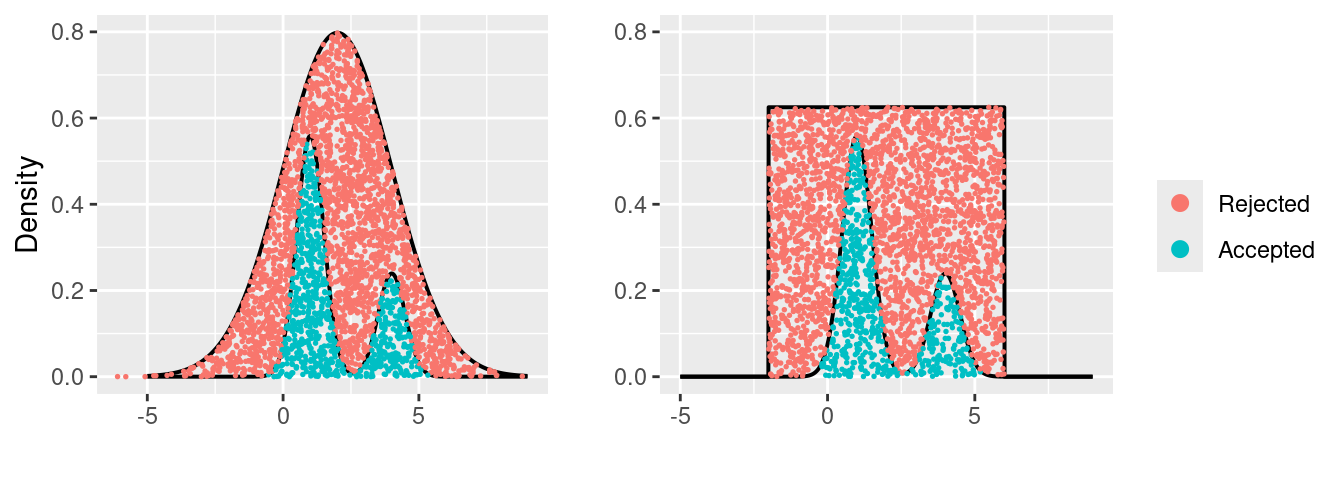
Is the Bayesian solution to estimating the parameters really as simple as Monte Carlo? Not quite. The problem is that the inputs (the other parameters) defining any given full conditional distribution are actually unknown random quantities which must also be estimated. Returning to the example in Section 3.2.1, we have three unknown parameters, \(\eta\), \(\alpha\) and \(\beta\), of which the full conditionals depend on the other two. We can obtain a Monte Carlo sample for any one of these parameters by holding the other two fixed, but since these parameters are random quantities, we must account for the uncertainty of those inputs by updating them as new estimates become available – we cannot keep them fixed and expect the samples we generate to be accurate. But if we update the input parameters each time before making a draw from the full conditional, the generated sample will no longer be i.i.d.
Using the theory of Markov chains (see Section 3.3.3), Monte Carlo sampling techniques can be extended to provide samples from distributions conditional on other unknown parameters.
3.3.2 Markov Chain Monte Carlo Methods
The general idea of Markov chain Monte Carlo (MCMC) methods is to draw from each of the full conditional distributions in an iterative fashion, using the parameter estimates from the previous iteration as fixed value inputs into the full conditionals, ultimately providing an MCMC posterior sample. Unlike Monte Carlo methods, MCMC methods generate samples which are dependent rather than i.i.d. That is, MCMC algorithms generate a sequence of draws which are autocorrelated. However, once the Markov chain has converged, then subsequent draws should be (mostly) independent (see Section 3.3.4.2 for further discussion).
A general MCMC algorithm to update hypothetical parameters \(\bm{\theta} = (\theta_1, \ldots,\theta_H)\) is as follows:
- Initialise the first sample, \(\bm{\theta}^{(0)} = (\theta_1^{(0)}, \ldots,\theta_H^{(0)})\).
- For each iteration \(m=1,\dots,M\), update each of the parameters to get \(\bm{\theta}^{(m)} = (\theta_1^{(m)}, \ldots,\theta_H^{(m)})\) according to a particular MCMC method.
If the resulting Markov chain reaches stationarity, then there should be no dependence on the initial values. However, early draws will be dependent on these values and will lack convergence. It is therefore necessary to discard some portion of the start of the chain. This discarded portion is called the burn-in phase (see Section 3.3.4.2 for more details).
MCMC methods include Gibbs sampling (Geman and Geman 1984; Gelfand and Smith 1990), Metropolis-Hastings (Metropolis et al. 1953; Hastings 1970), adaptive rejection sampling (Gilks and Wild 1992; Gilks, Best, and Tan 1995), Hamiltonian (hybrid) Monte Carlo sampling (Duane et al. 1987), and slice sampling (Neal 2003). Some of the more common MCMC methods are briefly described below.
Gibbs sampling simply draws from the full conditionals themselves, using standard Monte Carlo methods at each iteration (by holding the unknown parameters fixed, i.e. using their latest estimates). This assumes that the full conditionals are recognisable distributions for which Monte Carlo methods exist, which usually requires conjugate priors. Achieving conjugacy becomes more difficult with model complexity and higher dimensions, and conjugate priors are not necessarily a good choice.
The Metropolis-Hastings algorithm is essentially a Markov chain extension of accept-reject Monte Carlo sampling, except there is no need for the proposal to envelope the target distribution. Instead of drawing from the full conditional, candidate values are drawn from a proposal distribution which are either accepted or rejected. Finding a suitable proposal distribution can be difficult (especially for multivariate distributions). An ideal proposal distribution should be easy to sample from and have a similar shape to the target distribution (the full conditional). The Gaussian distribution is a common choice, where the variance represents a tuning parameter, which can play a large role in the ability for the algorithm to explore the posterior surface, the acceptance/rejection rate, and the rate of convergence.
Adaptive rejection sampling combines the ideas of an envelope function, accept-reject sampling, and the inverse CDF method. This method requires that the full conditional is log-concave. A piece-wise linear upper bound (and optionally a lower bound) is constructed for the log-full conditional which consists of intersecting tangents at a specific number of starting points (new points are added to this set of starting points when a draw is rejected). The inversion method is then used to draw samples from the exponentiated upper bound function, and an auxiliary variate is used to determine if the sample is accepted or rejected, as in the Monte Carlo accept-reject method. When a point is rejected, a new tangent is (potentially) added 1 at that point which decreases the rejection rate for future samples close to that part of the domain. This approach can be quite efficient for a rejection based sampler, and is the primary sampling method used by the software WinBUGS 2.
Further reading:
- C. Robert and Casella (2011): a historical review of the development of MCMC and key milestones and advances that makes Bayesian inference possible today.
- Cappe and Robert (2000): a historical review of and introduction to the key components of MCMC.
- C. P. Robert (2016): a good introduction to the Metropolis-Hasting algorithm with example R code and references to recent extensions of the methodology.
- Betancourt (2017): a theoretical introduction to Hamiltonian Monte Carlo.
- Rogozhnikov (2016): an interactive website that demonstrates Hamiltonian Monte Carlo in action.
3.3.3 Markov Chains and the Markov Property
A Markov chain is a discrete-space stochastic process with the Markov property. “Discrete-space” refers to the fact the Markov chain is comprised of discrete steps (iterations). The parameters being estimated at each iteration are random, so the process being generated by an MCMC algorithm is stochastic (random). And the Markov property refers to the lack of dependence between new and preer, the observance of this property is usually delayed by a lag of so many iterations. Formally, using the notation from Section 3.3.2, the chain of estimates for parameter \(\theta\) has the Markov property if
\[p(\theta^{(m)}|\theta^{(0)}, \ldots, \theta^{(m-1)}) = p(\theta^{(m)}|\theta^{(m-1)}),\]
or put another way,
\[\text{Cor}\left(\left\{ \theta^{(0)}, \ldots, \theta^{(m-1)}\right\}, \left\{ \theta^{(1)}, \ldots, \theta^{(m)}\right\} \right) \approx 0.\]
Sometimes the autocorrelation may persist for several iterations, known as the lag. For lag \(l\), the chain for \(\theta\) has the Markov property if
\[p(\theta^{(m)}|\theta^{(0)}, \ldots, \theta^{(m-1)}) = p(\theta^{(m)}|\theta^{(m-l)}, \ldots, \theta^{(m-1)}).\]
It is desirable for this lag value to be as close to 1 as possible. This Markov property is important because it means the chains are not dependent on the initial values and are exploring the posterior surface well. Together with some mild assumptions (Hammersley and Clifford 1971; Besag 1974), the Markov chain will converge to a stationary distribution which is the posterior distribution (Geman and Geman 1984).
If there is substantial autocorrelation, this reduces the effective sample size (ESS). Various definitions of ESS exist. One example is
\[
ESS = \frac{M}{1 + 2\sum_{l=1} \rho(l)}
\]
where \(\rho(l)\) is the sample autocorrelation of a given parameter at lag \(l\). A robust and easy way to compute ESS in R is via the effectiveSize function from the coda package.
Ideally, the ESS is equal or very close to \(M\). One remedy for addressing autocorrelation between samples is thinning (see Section 3.3.4.2).
3.3.4 Software and Computation
3.3.4.1 Software
There are many software programs available for implementing Bayesian hierarchical models. Commonly used software includes WinBUGS (D. J. Lunn et al. 2000) and its open-source successor OpenBUGS (D. Spiegelhalter et al. 2014), JAGS (Plummer 2003, 2017), Stan (Carpenter et al. 2017; Stan Development Team 2018b), and INLA (Rue, Martino, and Chopin 2009). Note that INLA uses Laplace approximations to estimate the posterior, while the other four use MCMC simulation. All of these software have corresponding libraries in R (R Core Team 2018) so that they can be interfaced with R, facilitating the statistical analysis process after the posterior has been estimated. The R packages and the primary interfacing function are:
- WinBUGS:
R2WinBUGS::bugs()(Sturtz, Ligges, and Gelman 2005). - OpenBUGS:
R2OpenBUGS::bugs()(Sturtz, Ligges, and Gelman 2010). - JAGS:
R2jags::jags()(Su, Y.-S. and Yajima, M. 2015) orrjags::coda.samples()(Plummer 2011) orrunjags::run.jags()(Denwood 2016). - Stan:
rstan::stan()(Stan Development Team 2018a). - INLA:
INLA::inla()(Martins and Rue 2013; Lindgren and Rue 2015).
Note: All R packages above are available on the Comprehensive R Archive Network (CRAN) except for INLA. This can be installed using the following R code:
install.packages("INLA", repos = c(getOption("repos"), INLA = "https://inla.r-inla-download.org/R/stable"), dependencies = TRUE)A worked example demonstrating how to use OpenBUGS to implement a Bayesian model is provided in Appendix A.3.
There also exists packages like CARBayes which can implement select types of models independently, that is, without the need for additional software programs. Examples of fitting Bayesian spatial models using CARBayes is provided in Chapter 4.
3.3.4.2 Burn-in and Thinning
When an MCMC method is used to estimate the posterior, it is necessary to discard the initial portion of the Markov chain, called the burn-in. This is because the chains need to be initialised with random values, and unless those initial values lie within a high-density region of the parameter space, then subsequent draws from the full conditional distributions will not be representative of the true posterior. In other words, the distribution of values generated by the chain has not yet converged to the stationary distribution. Provided the initial values are not too far from the posterior mode(s), the chain should eventually converge. The number of iterations to discard as burn-in depends on the initial values and the model complexity (number of parameters), but usually it is sufficient to discard between 2,000 and 50,000 iterations.
Regardless of how quickly the chain achieves stationarity, a second issue with MCMC samplers is that the resulting output is inherently autocorrelated. This means the values generated at each iteration depend on the values generated at previous iteration(s). This is problematic since the goal is to generate independent samples. This issue is directly related to the mixing rate, which refers to how efficiently the posterior surface is explored. Accept-reject samplers like the Metropolis-Hastings algorithm which have a high rejection rate or samplers that move too slowly through the parameter space produce highly auto-correlated samples and result in slow-mixing. If the autocorrelation between the set of estimates of a particular parameter is large for lag values greater than 1 (see Section 3.3.3), then a common solution is to thin the MCMC sample by taking every \(k^{\text{th}}\) value, thereby reducing the dependency between successive draws, a practice known as “thinning.” However, this increases the computational cost k-fold to achieve the same posterior sample size.
3.3.4.3 Checking Convergence
To avoid drawing misguided conclusions based on biased, erroneous posterior estimates, it is important to check that the MCMC chains have converged. There are numerous diagnostic tests for assessing convergence. One of the simplest is Geweke’s convergence diagnostic (Geweke 1992). In essence, the MCMC chain of values is treated as a time series. If the time series is stationary, then the mean, variance, and autocorrelation structure ought to be the same for any given subset of that time series. For example, given a posterior sample of \(M\) iterations, say \(\bm{\theta} = \{\bm{\theta}^{(0)}, \ldots, \bm{\theta}^{(M)} \}\), then the first half of that chain \(\{\bm{\theta}^{(1)}, \ldots, \bm{\theta}^{(M/2)} \}\) should look similar to the second half \(\{\bm{\theta}^{(M/2+1)}, \ldots, \bm{\theta}^{(M)} \}\). Instead of halving the chain, Geweke recommended comparing the first 10% with the last 50%. Formally, the means of these two portions of the chain are compared using a standard z-score test statistic under the assumption that the two portions have the same mean.
Other examples of convergence diagnostics include that proposed by Raftery and Lewis (1996), Gelman and Rubin (1992), and Brooks and Gelman (1998). For a systematic review on some of the early diagnostics developed, see Cowles and Carlin (1996).
An informal but commonly used test is to construct trace plots for each parameter in each chain, or if there are many parameters, for selected parameters (usually more useful for those parameters higher in the model hierarchy). Trace plots are essentially line graphs where the x-axis represents the MCMC iterations and the y-axis represents the estimates of the parameters. The following example shows 4 chains for a hypothetical parameter, with initial values of -10, 0, 10, and 20.
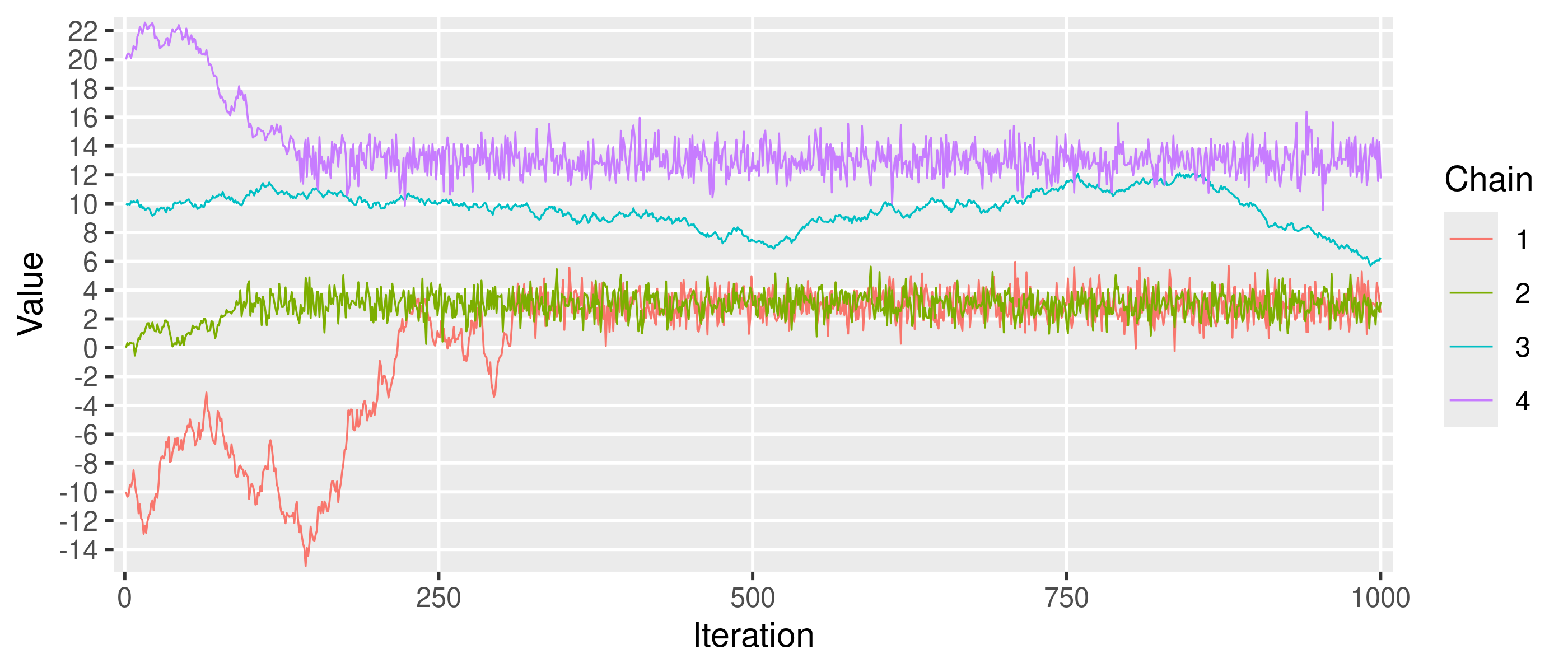
This trace plot indicates that chain 1 appears to converge to the stationary distribution which has a mean of around 3. Chain 2 appears to converge to the same stationary distribution at a slightly faster rate than chain 1. Chain 3 does not appear to have converged. Chain 4 appears to have converged to a different stationary distribution from chains 1 and 2, suggesting a second mode on the posterior surface. The existence of different stationary distributions can be indicative of a posterior which is genuinely multimodal, perhaps due to important explanatory variables missing from the model, or of a chain which has become stuck in a local mode and is therefore unable to fully explore the posterior surface. Although such a chain has technically converged, it is not ideal behaviour as the sample is not representative of the true posterior. Such results should be investigated further. Two possible courses of action are running the chains for longer and adjusting tuning parameters (in the case of samplers like the Metropolis-Hasting algorithm).
3.4 Bayesian Inference
3.4.1 Summarising the Posterior
Once we have a posterior sample, the next step towards making statistical inference about the unknown parameters is to summarise the posterior. If the parameters have been estimated using MCMC, then the posterior sample can be summarised using sample statistics such as the mean, variance, and various quantiles.
Suppose we have a posterior sample for an \(N\)-dimensional parameter \(\bm{\theta}\) stored in R as an \(M \times N\) matrix, where \(M\) is the number of MCMC iterations. This can be summarised by applying the relevant function over the columns (margin = 2) as follows:
apply(theta, margin = 2, mean)
apply(theta, margin = 2, var)
apply(theta, margin = 2, median)
apply(theta, margin = 2, quantile, probs = c(0.05, 0.95))(Note that this produces very similar output to that obtained using print() on the OpenBUGS output as shown for the pumps example in Appendix A.3.) The last line represents a 90% confidence interval for \(\bm{\theta}\).
We can also create visual summaries of the marginal posterior distributions, using boxplots or empirical densities. For the pumps example in Appendix A.3, the failure rate \(\bm{\theta} = (\theta_1,\ldots,\theta_{10})\) can be visualised as follows:
library(tidyr)
library(ggplot2)
theta <- Pump.example$sims.list$theta
M <- nrow(theta)
N <- ncol(theta)
dat <- data.frame(iteration = 1:M, theta)
dat <- gather(dat, "var", "value", -iteration) # Long format
dat$var <- rep(1:10, each = M)
# Boxplot
ggplot(dat, aes(x = factor(var), y = value, group = var)) +
geom_boxplot() +
scale_x_discrete("Pump") +
scale_y_continuous("Failure rate")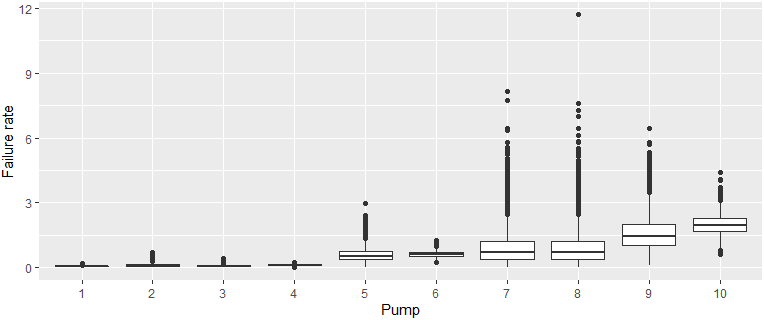
# Density
ggplot(dat, aes(x = value, group = var, fill = factor(var))) +
geom_density(alpha = 0.5, colour = NA) +
coord_cartesian(ylim = c(0, 5), xlim = c(0, 3.5)) +
scale_x_continuous("Failure rate", expand = c(0.01, 0.01)) +
scale_fill_discrete("Pump")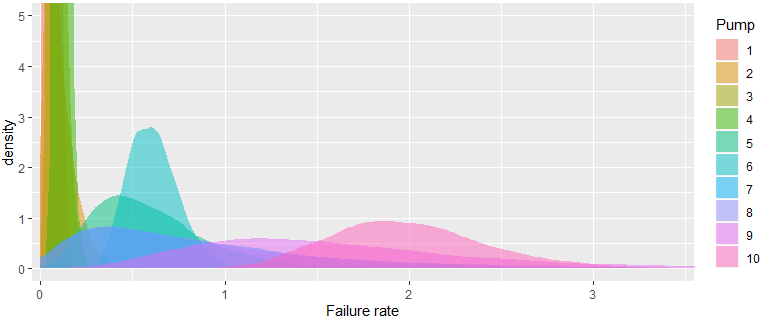
3.4.2 Making Inference
Based on summaries of the posterior distribution, we can make inferences about the process that gave rise to the data that we observed.
For the pumps example above, we can make statements like the following (note that the pumps are ordered by the observed failure rate, \(x/t\), which is also the order of the posterior median failure rate):
- The order of the posterior median failure rate is the same as the observed failure rate, \(x/t\). (Compare
order(data$x / data$t)withorder(apply(theta, 2, median).) That is, according to this statistic, pump 1 has the best performance, and pump 10 has the worst performance. Note that the order of performance of pumps 2 and 3 swap if we consider the mean failure rate instead,order(apply(theta, 2, mean), due to the skewness of the posterior distribution for pump 2. - The failure rate for the first 4 pumps is similarly low, based on the summary plots and 95% credible intervals. So the differences in failure rates between these pumps is negligible (not significant). Using 90% credible intervals, however, pump 1 would be considered substantively better than pump 4.
- With a posterior mean failure rate of about 0.0599, pump 1 is expected to fail once about every 16,700 hours of operation (recall that \(t\) was measured in 1000s of hours). More generally, the expected time between failures for each pump is given by the reciprocal of the mean failure rate, i.e.
1/apply(theta, 2, mean).
3.4.3 Model Evaluating
Before making any inference, in addition to checking for convergence, we also need to check that the model fits the data well. The adage “garbage in, garbage out” is relevant: if the model does not fit the data, then replicated data generated from the model using the estimates to evaluate the likelihood will produce values that are dissimilar to the observed data and lead to poor model predictions.
Common measures of Bayesian model fit include:
- the Bayesian information criterion (BIC) (Gideon 1978);
- the deviance information criterion (DIC) (D. J. Spiegelhalter et al. 2002); and
- the Watanabe-Akaike (or widely applicable) information criterion (WAIC) (Watanabe 2010, 2013).
The WAIC is closely related to the more widely known DIC measure, which is based on a deviance, defined by:
\[ D(\bm{\theta}) = -2 \log{p(\bm{y}|\bm{\theta})} + 2 \log{h(\bm{y})} \]
where \(h(\bm{y})\) is some standardising term, which is a function of the data only. The value of \(h(\bm{y})\) doesn’t really matter for model comparison, since it doesn’t depend on the parameters (which may differ between models), but rather only the data (which should be the same across the models being compared). So for convenience, we typically set \(h(\bm{y})=1\) so that the term \(2\log{h(\bm{y})}=0\). In this case, the deviance simplifies to
\[ D(\bm{\theta}) = -2 \log{p(\bm{y}|\bm{\theta})}. \]
The effective dimension, \(p_D\), is defined as
\[ p_D = \overline{D(\bm{\theta})} - D(\tilde{\theta}) \]
where \(\overline{D(\bm{\theta})}\) is the posterior mean deviance
\[\begin{align*} \overline{D(\bm{\theta})} = & \text{E}_{\bm{\theta}}\left\{D(\bm{\theta}|\bm{y})\right\} \\ = & \text{E}_{\bm{\theta}}\left\{-2 \log{p(\bm{y}|\bm{\theta})}|\bm{y} \right\} \end{align*}\]
which can be regarded as a Bayesian measure of fit, and \(\tilde{\theta}\) is an estimate of \(\bm{\theta}\) depending on \(\bm{y}\). The DIC described by D. J. Spiegelhalter et al. (2002) is defined as:
\[\begin{align*} \text{DIC} = & \overline{D(\bm{\theta})} + p_D \\ = & \overline{D(\bm{\theta})} + \overline{D(\bm{\theta})} - D(\tilde{\theta}) \\ = & 2\overline{D(\bm{\theta})} - D(\tilde{\theta}) \\ = & 2\left[\text{E}_{\bm{\theta}}\left\{-2 \log{p(\bm{y}|\bm{\theta})}|\bm{y} \right\} \right] - \left[-2\log{p(\bm{y}|\tilde{\theta})}\right] \\ = & -4\text{E}_{\bm{\theta}}\left\{\log{p(\bm{y}|\bm{\theta})}|\bm{y} \right\} + 2\log{p(\bm{y}|\tilde{\theta})} \end{align*}\]
A natural choice for \(\tilde{\theta}\) is the posterior mean \(\bar{\theta} = \text{E}_{\bm{\theta}}(\bm{\theta}|\bm{y})\). Alternative versions of the DIC were proposed by Celeux et al. (2006).
However, the DIC can also be expressed in terms of the effective dimension, \(p_D\). Starting from the third line in the equation above:
\[\begin{align*} \text{DIC} = & 2\overline{D(\bm{\theta})} - D(\tilde{\theta}) \\ = & 2p_D + D(\tilde{\theta}) \\ = & 2p_D - 2\log{p(\bm{y}|\tilde{\theta})}. \end{align*}\]
This second expression demonstrates the relation to WAIC more readily. In general, the WAIC is defined as:
\[ \text{WAIC} = 2p_{WAIC} - 2\text{LPPD}. \]
The second term in DIC is \(\log{p(\bm{y}|\tilde{\theta})}\) where \(\tilde{\theta}\) is a point estimate of \(\bm{\theta}\). For WAIC, this term is replaced by the log pointwise predictive density (LPPD), defined as:
\[\begin{align*} \text{LPPD} = & \log \prod_{i=1}^N p_{\text{post}}(y_i) \\ = & \log \prod_{i=1}^N \text{E}_{\text{post}}\left[p(y_i | \theta_i) \right] \\ = & \log \prod_{i=1}^N \text{E}_{\bm{\theta}}\left[p(y_i | \theta_i)| y_i \right] \\ \approx & \sum_{i=1}^N \log \frac{1}{M} \sum_{m=1}^M p\left(y_i | \theta_i^{(m)}\right). \end{align*}\]
Just like DIC, there are variants of WAIC which depend on how \(p_{WAIC}\) is defined. Gelman, Hwang, and Vehtari (2014) also propose two variants:
\[ p_{WAIC~1} = 2 \sum_{i=1}^N \left\{ \log \text{E}_{\text{post}}\left[p(y_i | \theta_i) \right] - \text{E}_{\text{post}}\left[\log p(y_i | \theta_i) \right]\right\} \]
and
\[ p_{WAIC~2} = \sum_{i=1}^N \text{Var}_{\text{post}}\left[\log p(y_i | \theta_i) \right]. \]
Although DIC is a commonly used measure to compare Bayesian models, WAIC has several advantages over DIC, including that it closely approximates Bayesian cross-validation, it uses the entire posterior distribution and it is invariant to parameterisation (Vehtari, Gelman, and Gabry 2017). The WAIC is a more fully Bayesian approach for estimating out-of-sample expectation (Gelman, Hwang, and Vehtari 2014).
Sample R code for computing the WAIC from an MCMC posterior sample is provided in Section 6.1.
3.4.4 Advantages of Bayesian Inference
There are a number of advantages to using Bayesian techniques over classical techniques to estimate parameters and make statistical inference. Here are some of the main advantages (this is not an exhaustive list!):
- If one obtains more data, one does not have to redo the entire analysis. If the posterior from the initial analysis can be computed analytically, then this distribution simply becomes the prior for the subsequent analysis. For example, in Section 3.2.1, the new prior for \(\eta\) would be \(\text{Gamma}(\eta;\alpha+\sum_{i=1}y_i,\beta+N)\) where \(y_1,\ldots,y_N\) was the original sample, and the likelihood \(\text{Poisson}(y^*;\eta)\) would reflect the new sample of data \(y^*=y_1^*,\ldots,y_n^*\). Similarly for the worked example in Appendix A.2, the original posterior \(\text{Beta}(\theta|y+\alpha,n-y+\beta)\) would become the new prior for \(\theta\). In practice, when using MCMC estimation techniques, this means using the same prior(s) (i.e. the same distributional form), but updating the parameters using sufficient statistics from the original posterior 3.
- Bayesian models may appear daunting due to the complex hierarchical structure, but actually this is a major advantage: it allows us to fit models to very complex processes, and the hierarchical structure is a natural way to emulate a huge variety of processes. This is especially true for spatial and spatio-temporal processes, which are inherently hierarchical and exhibit autocorrelation – a difficulty readily addressed by Bayesian hierarchical models through use of purposefully constructed prior distributions. (We have so far omitted discussion of spatial models as this will be covered in more depth throughout the remainder of this document, especially Chapters 4 and 5).
- In addition to the hierarchical structure, Bayesian models permit a wide variety of types of models (e.g. regression models, mixture models, multi-level models, etc.), and model specifications, in terms of specifying the priors and hyperpriors, and the variety of distributions available, including non-standard distributions. Non-standard likelihood functions (and even likelihood-free methods) are also possible.
- Use of prior distributions helps accommodate for the uncertainty of the unknown parameters and allows for a priori knowledge to be incorporated into the model in a formal way. This is sometimes criticised for introducing subjectivity rather than “letting the data speak for themselves,” but thoughtfully chosen priors are arguably more appropriate than assuming uniform probability of outcomes (which is essentially the classical approach), and given sufficient data, the prior distributions should not have an undue influence on the posterior.
- Bayesian analyses provide a distribution rather than a point estimate for each parameter, which is more informative and better reflects the uncertainty of the estimates. Bayesian inference is very straightforward from the marginal posterior distributions, as demonstrated in Sections 3.4.1 and 3.4.2.
The main disadvantage of Bayesian methods is that they are typically computationally slow. However, Bayesian methods are continuously being improved, and some of the computational methods can be comparatively fast. It may also be difficult to choose appropriate priors and assess convergence. However, these challenges are arguably easier to overcome than those arising from classical estimation methods, in part due to the growing literature which provides guidance on these issues.
References
The number of tangents may be capped, otherwise using too many tangents can be computationally more expensive than rejecting samples.↩︎
Note that there are several variations of this algorithm, including a derivative-free version (i.e. uses chords instead of tangents), and several other generalisations (e.g. concave-convex adaptive rejection sampling (Görür and Teh 2011)). WinBUGS uses a derivative-free variation.↩︎
For example, if the posterior for the worked example in Appendix A.2 was not known to be \(\text{Beta}(\theta|y+\alpha,n-y+\beta)\), but one had an MCMC sample from this posterior, then the posterior sample mean and variance, say \(m\) and \(v\), can be used to find the parameters \(a^*\) and \(b^*\) such that \(\text{Beta}(\theta|a^*,b^*)\) reflects the updated prior. Specifically, \(a^* = \frac{m(m-m^2-v)}{v}\) and \(b^* = a^*/m - a^*\).↩︎